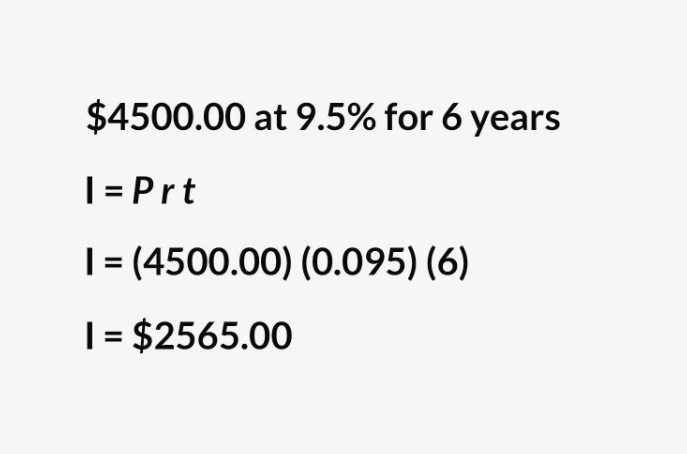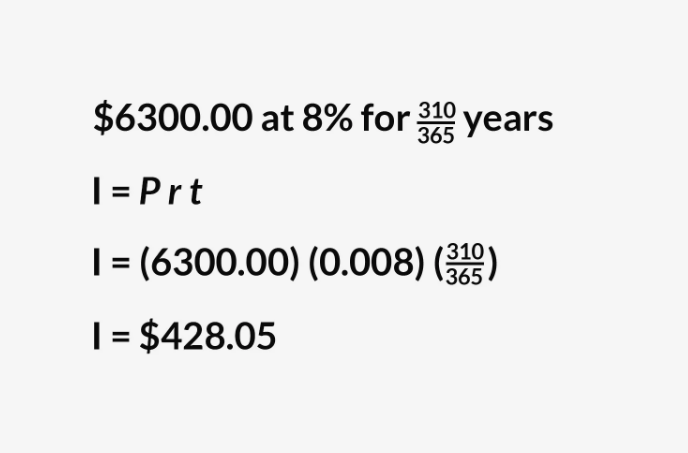Khi bạn vay tiền từ ngân hàng , bạn phải trả lãi. Bản chất của tiền lãi thực ra chính là một khoản phí được tính cho việc vay tiền. Tỷ lệ % tiền lãi được tính tùy vào số tiền gốc trong một khoảng thời gian nhất định, thường là một năm. Tùy thuộc vào quy ước ban đầu rằng bạn sẽ trả lãi theo định kỳ (lãi đơn) hay sẽ trả vào cuối kỳ vay (lãi kép) mà số tiền phải trả là khác nhau. Để giúp bạn hình dung rõ hơn, bài viết dưới đây sẽ mô tả, lấy ví dụ cụ thể, đơn giản trong từng trường hợp một cách dễ hiểu nhất về lãi đơn và lãi kép, hãy cùng chúng tôi tìm hiểu nhé!
Tóm tắt nội dung
Lãi suất kép là gì? Công thức, định nghĩa và ví dụ
Lãi suất kép là gì?
Tiền lãi kép nghe thì có vẻ phức tạp, nhưng hiểu một cách đơn giản thì nó chính là khoản tiền lãi được trả cho cả tiền gốc và lãi lũy kế. Nếu bạn muốn biết bạn sẽ kiếm được bao nhiêu tiền lãi cho khoản đầu tư của mình hoặc nếu bạn muốn biết bạn sẽ phải trả thêm bao nhiêu so với số tiền gốc cho khoản vay hoặc thế chấp, bạn cần phải hiểu cách thức hoạt động của lãi kép, lãi đơn. Những thông tin cơ bản dưới đây sẽ giúp bạn hiểu rõ hơn.
Ví dụ đơn giản về lãi suất kép
Để hiểu rõ hơn về lãi suất kép, bạn có thể xem ví dụ đơn giản sau: Nếu bạn bắt đầu với 100 đô la và bạn nhận được 10 đô la tiền lãi vào cuối giai đoạn đầu tiên, bạn sẽ có 110 đô la mà bạn có thể kiếm được tiền lãi trong giai đoạn thứ hai. Vì vậy, trong giai đoạn thứ hai, bạn sẽ kiếm được 11 đô la tiền lãi. Bây giờ cho giai đoạn thứ 3, bạn có 110 + 11 = 121 đô la mà bạn có thể kiếm được tiền lãi. Vì vậy, vào cuối giai đoạn 3, bạn sẽ kiếm được tiền lãi trên 121 đô la. Số tiền sẽ là 12,10. Vì vậy, bây giờ bạn có 121 + 12,10 = 132,10 có thể kiếm được tiền lãi.
Công thức dưới đây sẽ giúp bạn tính toán tổng số tiền lãi trong toàn bộ thời gian gửi hoặc vay trong một bước, thay vì phải tính từng bước 1 như trên.
Công thức tính lãi kép
Lãi kép được tính dựa trên tổng số tiền gốc, % lãi suất (APR hoặc tỷ lệ phần trăm hàng năm) và thời gian liên quan. Giả sử ta gọi:
- P là tổng số tiền gốc (số tiền ban đầu bạn vay hoặc gửi).
- r là lãi suất hàng năm (phần trăm).
- n là số năm số tiền được gửi hoặc mượn.
- A là số tiền tích lũy sau n năm, bao gồm cả lãi.
Khi đó số tiền lãi sau n năm sẽ là:
A = P (1 + r)n
Giả sử, nếu bạn vay trong 5 năm, công thức sẽ như sau:
A = P (1 + r)5
Công thức này áp dụng cho cả tiền đầu tư và tiền vay.
Trường hợp trả lãi thường xuyên
Nếu lãi được trả thường xuyên hơn thì sao? Nó không phức tạp hơn nhiều so với ở trên, ngoại trừ tỷ lệ phần trăm thay đổi. Dưới đây là một vài công thức ví dụ:
Hàng năm = P × (1 + r) = (trả lãi kép hàng năm)
Hàng quý = P (1 + r / 4) 4 = (trả lãi kép hàng quý)
Hàng tháng = P (1 + r / 12) 12 = (trả lãi kép hàng tháng)
Bảng tính lãi kép
Bảng tính giúp bạn kiểm tra cách hoạt động của lãi kép một cách đơn giản và giúp bạn kiểm soát tốt hơn khoản vay hay khoản đầu tư của mình. Giả sử bạn bắt đầu với 1000 đô la và lãi suất là 10%. Nếu bạn trả lãi đơn (không phải lãi kép), vào cuối năm đầu tiên bạn sẽ phải trả 1000 đô la + 10% (tức là 100 đô la khác) và tổng số tiền sẽ là 1100 đô la. Vào cuối 5 năm, tổng số tiền lãi đơn sẽ là $ 1500.
Số tiền bạn phải trả với lãi kép tùy thuộc vào mức độ bạn trả hết khoản vay. Nó chỉ có 1100 đô la vào cuối năm đầu tiên, nhưng lên đến hơn 1600 đô la sau 5 năm. Nếu bạn gia hạn thời gian cho vay, số tiền có thể tăng lên nhanh chóng, cụ thể:
| Năm | Khoản vay ban đầu | Tổng lãi suất hàng năm | Khoản vay cuối kỳ |
| 0 | $ 1000,00 | $ 1.000,00 × 10% = $ 100,00 | $ 1,100,00 |
| 1 | $ 1100,00 | $ 1,100,00 × 10% = $ 110,00 | $ 1,210,00 |
| 2 | $ 1210,00 | $ 1,210,00 × 10% = $ 121,00 | $ 1,31,00 |
| 3 | $ 1331,00 | $ 1,31,00 × 10% = $ 133,10 | $ 1.464.10 |
| 4 | $ 1464,10 | $ 1.464.10 × 10% = $ 146,41 | $ 1.610,51 |
| 5 | $ 1610,51 |
Một số công thức tính lãi suất đơn thường gặp
Lãi đơn không phức tạp như lãi kép mà đơn giản hơn nhiều. Tuy nhiên với nhiều người chưa rõ thì nghe khá khó hiểu. Chung quy lại, tính lãi đơn hoặc số tiền gốc, tiền lãi hoặc thời gian vay có vẻ khó hiểu, nhưng thực sự không khó như bạn nghĩ. Dưới đây là các ví dụ về cách sử dụng công thức lãi suất đơn để tìm một giá trị miễn là bạn biết các giá trị khác.
Tính lãi: với tiền gốc, tỷ lệ và thời gian đã biết
Khi bạn đã biết số tiền gốc, tỷ lệ lãi suất và thời gian vay (hoặc cho vay), số tiền lãi có thể được tính bằng cách sử dụng công thức:
I = Prt
Áp dụng với ví dụ trên, bạn có 4500 đô la để đầu tư (hoặc vay) với tỷ lệ lãi suất là 9,5% trong khoảng thời gian sáu năm. Tổng tiền lãi bạn phải trả sau 6 năm sẽ là:
I = 4500 đô la * 9,5% * 6 năm = 2565 đô la.
Tính lãi khi thời gian được tính bằng ngày
Giả sử bạn muốn vay $ 6300 từ ngày 15 tháng 3 năm 2004, cho đến ngày 20 tháng 1 năm 2005, với lãi suất 8 phần trăm. Công thức vẫn sẽ là I = Prt ; tuy nhiên, bạn cần tính toán theo đơn vị ngày.
Để tính được lãi, bạn phải xác định được tổng số ngày vay (hoặc được trả lại) số tiền. Cụ thể: Tháng 3 = 16 ngày, Tháng 4 = 30, Tháng 5 = 31, Tháng 6 = 30, Tháng 7 = 31, Tháng 8 = 31, Tháng 9 = 30, Tháng 10 = 31, Tháng 11 = 30, Tháng 12 = 31, Tháng 1 = 19. Do đó, tổng thời gian là 310/365 (Tổng cộng có 310 ngày trong số 365). Số này được nhập vào t trong công thức trên. Cụ thể ta có số lãi sẽ là:
Tổng tiền lãi khi vay 890 đô la với lãi suất 12,5% trong 261 ngày là bao nhiêu?
Một lần nữa, áp dụng công thức: I = Prt
Với t = 261/365 ngày. Ta có:

Tìm số vốn bỏ ra khi bạn biết tổng tiền lãi thu về, tỷ lệ lãi và thời gian
Giả sử, số tiền lãi thu về là 175,5 đô la với mức lãi suất 6,5% trong 8 tháng. Khi đó, để tính được tổng tiền vốn bỏ ra, bạn chỉ cần biến đổi công thức: I = Prt thành P = I/rt, cụ thể:
Số tiền bạn có thể đầu tư trong 300 ngày với lãi suất 5,5% để kiếm được 93,8 đô la?
Trong trường hợp này, bạn có 300 ngày, vậy nên t trong công thức sẽ bằng 300/365. Nhớ chuyển 365 thành tử số để công thức có thể hoạt động.
Bạn cần mức lãi suất hàng năm làm bao nhiêu với khoản đầu tư 2100 đô la để kiếm 122,5 đô la trong 14 tháng?
Từ công thức I=Prt suy ra: r=I/Pt trong đó, t = 14/12 tháng.
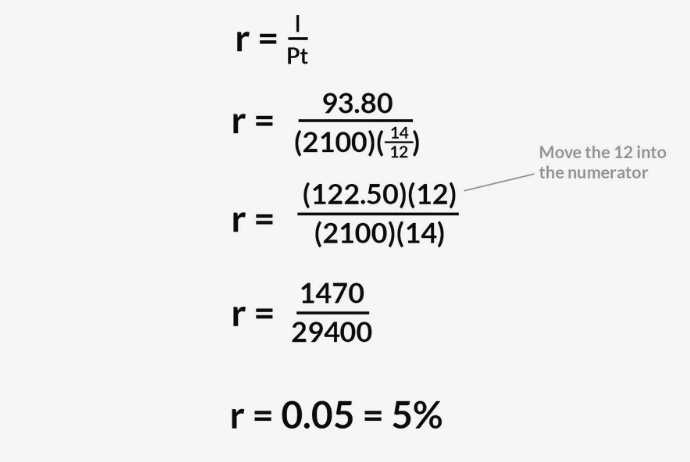
Như vậy, trên đây là toàn bộ những thông tin cơ bản, những ví dụ đơn giản và dễ hiểu nhất về lãi đơn và lãi kép. Hy vọng đến đây bạn đã có thể hiểu về 2 khái niệm này một cách rõ ràng và đã có thể tự tính toán được số lãi thu được hay số lãi sắp phải trả cho các khoản đầu tư hay khoản vay của cá nhân mình!