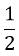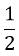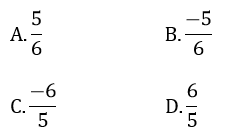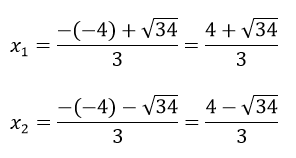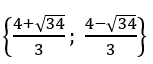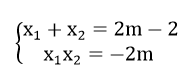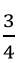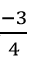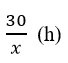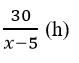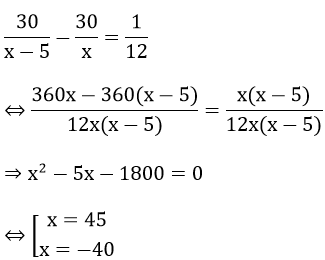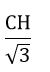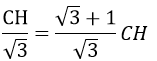Thời gian làm bài: 120 phút
Tóm tắt nội dung
Phần I. Trắc nghiệm (2 điểm)
Câu 1: Trong các đường thẳng sau đây, đường thẳng nào đi qua điểm A (1; 3):
A. x – y = 3 B. 2x + y =5
C. 2x – y = 3 D. x + y = 5
Câu 2: Điều kiện xác định của biểu thức 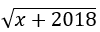
A. x = -2018 B. x ≠ -2018
C. x ≥ -2018 D. x ≤ -2018
Câu 3: Tìm m để 2 đường thẳng sau cắt nhau tại 1 điểm y = (2m – 1)x + 7 và y = 3x – 5
A. m = 2 B. m ≠ 2 C. m ≥ 2 D. m ≤ 2
Câu 4: Tìm giá trị của a để đồ thị hàm số y = ax2 đi qua điểm (1; – 4)
A. a = – 2 B. a = 2 C. a = 4 D. a = – 4
Câu 5: Biết phương trình x2 + bx – 2b = 0 có một nghiệm x = -3. Tìm nghiệm còn lại của phương trình:
Câu 6: Trong các nhận xét sau, nhận xét đúng là:
A. Hai cung bằng nhau thì có số đo bằng nhau
B. Hai cung có số đo bằng nhau thì bằng nhau
C. Cả a, b đều đúng
D. Cả a và b đều sai
Câu 7: Tính diện tích hình quạt có bán kính 6cm, độ dài cung là 5π cm
A. 10π cm2 B. 20π cm2 C.30π cm2 D. 15Bπ cm2
Câu 8: Tính diện tích toàn phần của hình nón có bán kính đáy 5 cm và độ dài đường sinh là 7 cm:
A. 35π cm2 B. 45π cm2 C. 52π cm2 D. 60π cm2
Phần II. Tự luận
Bài 1: (1,5 điểm) Giải các phương trình và hệ phương trình:
a) √5x – 2√5 = 0
b)3x2 – 8x – 6 = 0
Bài 2: (2 điểm)
1) Cho 2 hàm số (P): y = 2x2 và (d): y = -3x + 4
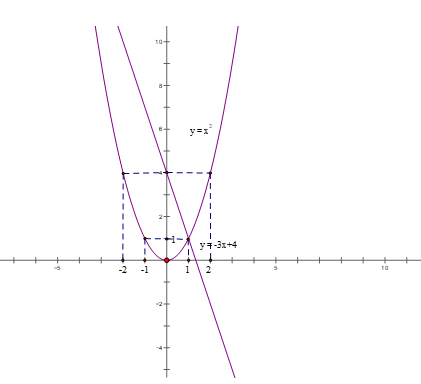
a) Vẽ 2 đồ thị trên cùng một mặt phẳng tọa độ Oxy
b) Tìm tọa độ giao điểm của 2 đồ thị trên bằng phép tính.
2) Cho phương trình x2 – 2(m – 1)x – 2m = 0.
Chứng minh rằng phương trình luôn có 2 nghiệm phân biệt với mọi m. Gọi 2 nghiệm của phương trình là x1; x2, tìm tất cả giá trị của m sao cho x12 + x1 – x2 = 5 – 2m
Bài 3: (1 điểm) Hai xe máy cùng xuất phát một lúc từ địa điểm A đến địa điểm B cách nhau 30 km. Xe thứ nhất chạy nhanh hơn xe thứ hai 5km/h nên đến B sớm hơn 5 phút. Tính vận tốc mỗi xe
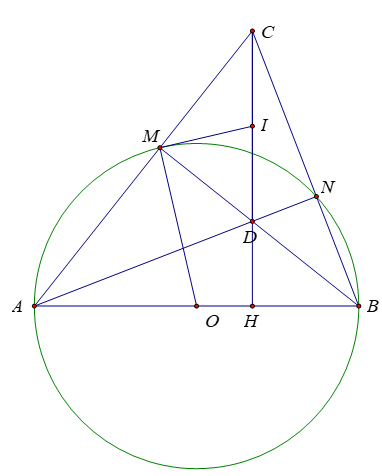
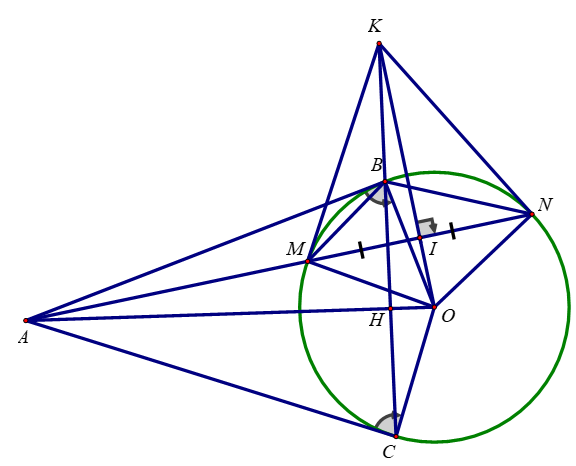
Bài 4: (3,5 điểm) Trên đường tròn (O; R) đường kính AB lấy 2 điểm M, N theo thứ tự A, M, N, B ( hai điểm M, N khác 2 điểm A và B). Các đường thẳng AM và BN cắt nhau tại C, AN và BM cắt nhau tại D
a) Chứng minh tứ giác MCND nội tiếp. Xác định tâm I đường tròn ngoại tiếp tứ giác
b) Gọi H là giao điểm của CD và AB. Chứng minh rằng:
BN.BC = BH.BAv
c) Tính ∠IMO
d) Cho biết ∠BAM = 45o; ∠BAN = 30o. Tính theo R diện tích của tam giác ABC
Phần I. Trắc nghiệm
| 1.B | 2.C | 3.B | 4.A |
| 5.D | 6.A | 7.C | 8.D |
Phần II. Tự luận
Bài 1:
a) √5x – 2√5 = 0
⇔ √5x = 2√5
⇔ x = 2
Vậy phương trình có nghiệm x = 2.
b)3x2 – 8x – 6 = 0
Δ’ = (-4)2 – 3.(-6) = 34 > 0
Phương trình có 2 nghiệm phân biệt
Vậy phương trình có tập nghiệm là S =
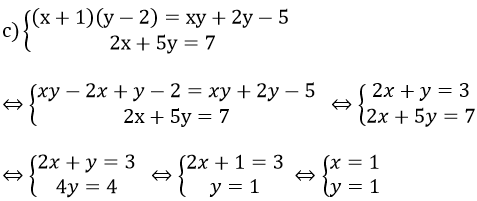
Vậy hệ phương trình đã cho có nghiệm (x; y) = (1; 1)
Bài 2:
1) Cho 2 hàm số (P): y = x2 và (d): y = -3x + 4
Xét hàm số: y = 2x2
Bảng giá trị
| x | -2 | -1 | 0 | 1 | 2 |
| y = 2x2 | 4 | 1 | 0 | 1 | 4 |
Đồ thị hàm số (P): y = x2 là đường parabol nằm phía trên trục hoành, nhận trục Oy là trục đối xứng và nhận đỉnh O (0;0) làm điểm thấp nhất
Xét hàm số y = -3x + 4
Bảng giá trị
| x | 0 | 1 |
| y = -3x + 4 | 4 | 1 |
b) phương trình hoành độ giao điểm của (P) và (d) là
x2 = – 3x + 4 ⇔ x2 + 3x – 4 = 0
=> phương trình có nghiệm x = 1 và x = – 4 ( do phương trình có dạng a + b + c =0)
Với x = 1 thì y = 1
Với x = – 4 thì y = 16
Vậy tọa độ giao điểm của (P) và (d) là (1; 1 ) và (-4; 16)
2) x2 – 2(m – 1)x – 2m = 0.
Δ’= (m-1)2 – (-2m) = m2 + 1 > 0 ∀m
Vậy phương trình luôn có 2 nghiệm phân biệt với mọi m
Theo định lí Vi- ét ta có:
⇔ x12 + x1 – x2 = 3 – (2m – 2)
⇔ x12 + x1 – x2 = 3 – x1 – x2
⇔ x12 + 2x1 – 3 = 0
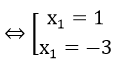
Với x1 = 1 thay vào phương trình ban đầu tìm được m =
Với x1 = -3 thay vào phương trình ban đầu, tìm đc m =
Vậy với m =
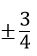 thì phương trình có 2 nghiệm thỏa mãn yêu cầu đề bài.
thì phương trình có 2 nghiệm thỏa mãn yêu cầu đề bài.Bài 3:
Gọi vận tốc xe thứ nhất là x ( km/h) (x > 5)
Vận tốc xe thứ hai là x – 5 (km/h)
Thời gian đi của xe thứ nhất là:
Thời gian đi của xe thứ hai là
Do xe thứ nhất đến B sớm hơn xe thứ hai 5′ =
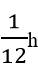 nên ta có phương trình
nên ta có phương trìnhVậy vận tốc của xe thứ nhất là 45 km/h
Vận tốc xe thứ hai là 40 km/h
Bài 4:
a) Ta có:
∠AMB = 90o (góc nội tiếp chắn nửa đường tròn)
=> ∠DMC = 90o
∠ANB = 90o (góc nội tiếp chắn nửa đường tròn)
=> ∠DNC = 90o
Xét tứ giác MCND có:
∠DMC + ∠DNC = 90o + 90o = 180o
=> Tứ giác MCDN là tứ giác nội tiếp
Do ∠DMC = 90o nên DC là đường kính đường tròn ngoại tiếp tứ giác MCDN
Do đó tâm I của đường tròn ngoại tiếp tứ giác là trung điểm I của DC
b) Xét tam giác CAB có:
AN ⊥ BC
BM ⊥ AC
AN giao với BM tại H
=> H là trực tâm của tam giác CAB
=> CH ⊥ BA
Xét ΔCHB và ΔBNA có:
∠CBA là góc chung
∠CHB = ∠ANB = 90o
=>ΔCHB ∼ ΔANB
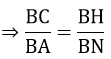 => BN.BC = BA.BH
=> BN.BC = BA.BHc) Xét tam giác HDB vuông tại H có:
∠BDH + ∠DBH = 90o (1)
Xét tam giác IDM cân tại I (ID = IM )
=> ∠IMD = ∠IDM
Mà ∠IDM = ∠BDH (đối đỉnh)
=> ∠IMD = ∠BDH (2)
Mặt khác tam giác OBM cân tại O ( OB = OM)
=> ∠OMB = ∠DBH (3)
Từ (1); (2) và (3)
=> ∠IMD + ∠OMB = ∠BDH + ∠DBH = 90o
=> ∠IMO = 90o
d) Xét tam giác BAN vuông tại N có:
∠NAB = 30o => ∠NBA = 60o
Xét tam giác CHB vuông tại H có ∠NBA = 60o
=> BH = CH.cot60o =
Lại có: Tam giác CHA vuông tại H có ∠CAH = 45o
=> Tam giác CHA vuông cân tại H => CH = HA
Ta có:
AB = HA + HB = CH +
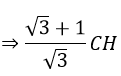 = 2R => CH = R√3(√3-1)
= 2R => CH = R√3(√3-1)Diện tích tam giác ABC là:
SABC =