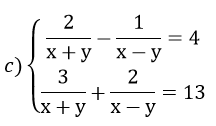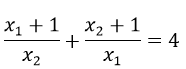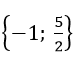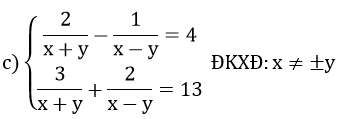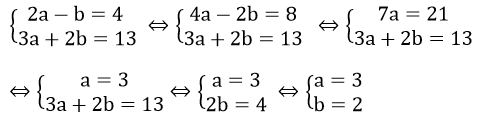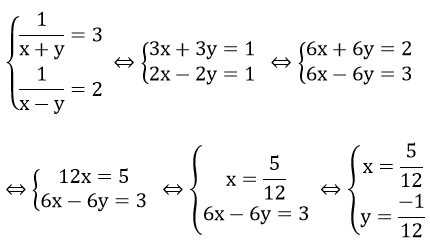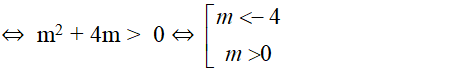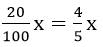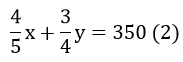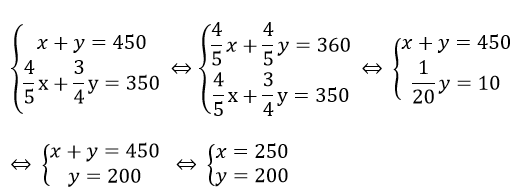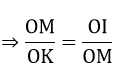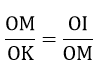Thời gian làm bài: 120 phút
Tóm tắt nội dung
Phần I. Trắc nghiệm (2 điểm)
Câu 1: Trong các phương trình sau; phương trình nào là phương trình bậc hai một ẩn
A. x2 + 2y = 4 B. 2x + y = 3
C. x2 + 3 x – 6 =0 D. x2 + y2 =5
Câu 2: Cho hàm số bậc nhất y = (m2 + 1)x – 5 và y = 5x +3. Tìm m để hai đường thẳng trên song song với nhau:
A. m = ±2 B. m = 2 C. m = – 2 D. m ≠ 2
Câu 3: Phương trình x2 + 2x + m + 2 = 0 có 2 nghiệm phân biệt khi
A. m > – 1 B. m < 1 C. m > 1 D. m < -1
Câu 4: Hệ phương trình 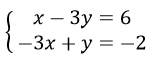
A. (-2; 0) B. (-2; 3) C. (0; -2) D. (0; 3)
Câu 5: Tổng 2 nghiệm của phương trình x2 + 7x – 5 = 0 là:
A. 7 B. -7 C. 5 D. -5
Câu 6: Cho đường tròn (O, R) và một dây cung AB = R. Khi đó số đo cung nhỏ AB là :
A. 60o B. 120o C. 150o D. 100o
Câu 7: Tính độ dài cung 60o của đường tròn có bán kính 3cm
A.2π cm B.π cm C. 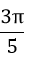
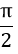 cm
cmCâu 8: Hình trụ có bán kính đáy là 2cm, chiều cao là 6 cm thì diện tích xung quanh là:
A.6π cm2 B.12π cm2 C.24π cm2 D.36π cm2
Phần II. Tự luận
Bài 1: (1,5 điểm) Giải các phương trình và hệ phương trình sau:
a) 2x2 -3x – 5 =0
b) x4 – 5x2 + 4 = 0
Bài 2: (1,5 điểm) Cho (P): y = x2 và đường thẳng (d) y = 2(m + 1)x + 2m – 1
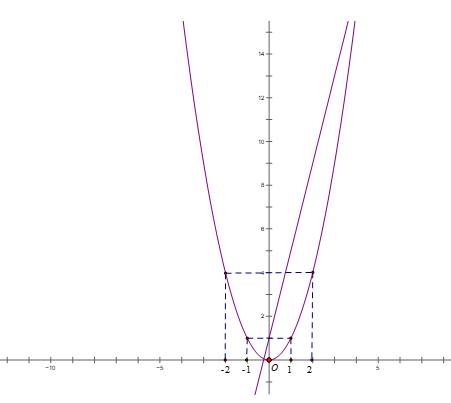
a) Khi m = 1, hãy vẽ (P) và (d) trên cùng một hệ trục tọa độ
b) Tìm m để x1, x2 thỏa mãn điều kiện sau:
Bài 3: (1,5 điểm) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình :
Sau khi xem bảng báo giá, mẹ của Hương đưa bạn 450 nghìn đồng nhờ bạn ra siêu thị mua một bàn ủi và một bộ lau nhà. Hôm nay đúng đợt khuyến mãi, bàn ủi được giảm 20%, bộ lau nhà được giảm 25% nên bạn Hương chỉ phải trả tổng cộng 350 nghìn đồng. Hỏi giá bán thực tế của bàn ủi và bộ lau nhà là bao nhiêu?
Bài 4: (3,5 điểm) Cho đường tròn (O; R) và điểm A nằm ngoài (O) sao cho OA = 3R. Vẽ các tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm). Vẽ cát tuyến AMN với (O) (M nằm giữa A và N và AMN không đi qua O). Gọi I là trung điểm của MN.
a) Chứng minh 5 điểm A, B, O, I, C thuộc một đường tròn
b) Chứng minh AM.AN = 8R2
c) Tính độ dài AM, AN khi MN = R√3
d) BC cắt OA, OI tại H và K
Chứng minh KM, KN là tiếp tuyến của (O)
Đáp án và Hướng dẫn giải
Phần I. Trắc nghiệm
| 1.C | 2.A | 3.D | 4.C |
| 5.B | 6.A | 7.B | 8.C |
Phần II. Tự luận
Bài 1:
a) 2x2 – 3x – 5 = 0
Δ = 32 – 4 . 2.(-5) = 49 > 0
Phương trình có 2 nghiệm phân biệt:
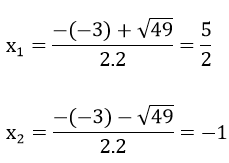
Vậy tập nghiệm của phương trình trên là S =
b) x4 – 5x2 + 4 = 0
Đặt t = x2 (t ≥ 0), khi đó phương trình trở thành:
t2 – 5t + 4 = 0
Phương trình có dạng a + b +c = 1+ (-5) + 4 = 0 nên phương trình có 2 nghiệm t1 = 1; t2 = 4
Với t1 = 1 thì x2 = 1 ⇔ x = ± 1
Với t1 = 4 thì x2 = 4 ⇔ x = ± 2
Vậy phương trình đã cho có tập nghiệm là S = {1; -1; 2; -2 }
Đặt
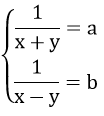 hệ phương trình trở thành:
hệ phương trình trở thành:Khi đó:
Vậy hệ phương trình đã cho có nghiệm (x; y) =
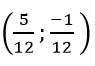
Bài 2:
a) Khi m =1, (d): y = 4x + 1
(P): y = x2
Bảng giá trị:
| x | -2 | -1 | 0 | 1 | 2 |
| y = x2 | 4 | 1 | 0 | 1 | 4 |
Đồ thị (P) là đường parabol nằm phía trên trục hoành, nhận trục Oy làm trục đối xứng, nhận O(0;0) là đỉnh và là điểm thấp nhất.
Vẽ đường thẳng (d): y = 4x + 1
Bảng giá trị
| x | 0 | -1 |
| y = 4x + 1 | 1 | -3 |
b) Phương trình hoành độ giao điểm của (P) và (d) là:
x2 = 2(m + 1)x + 2m – 1
⇔ x2 – 2(m + 1)x – (2m – 1) = 0 (*)
Δ’ = (m + 1)2 + (2m – 1)
= m2 + 2m + 1 + 2m – 1 = m2 + 4m
* Để đường thẳng d cắt (P) tại hai điểm phân biệt khi và chỉ khi phương trình có 2 nghiệm phân biệt hay Δ’ > 0
* Với m < – 4 hoặc m > 0 thì phương trình (*) có 2 nghiệm phân biệt. Theo định lí Vi-et ta có:

Kết hợp điều kiện, với 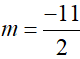
Bài 3:
Gọi giá tiền của bàn ủi khi chưa giảm giá là x ( nghìn đồng) (0 < x < 450)
Gọi giá tiền của bộ lau nhà khi chưa giảm giá là y ( nghìn đồng) (0 < x < 450)
Theo bài ra ta có: x + y = 450 (1)
Giá của bàn ủi khi giảm 20% là x –
Giá của bộ lau nhà khi giảm 25% là y –
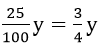
Do bạn Hương chỉ phải trả 350 nghìn đồng nên ta có phương trình
Từ (1) và (2) ta có hệ phương trình:
Vậy giá của bàn ủi khi chưa giảm giá là 250 nghìn đồng
Giá của bộ lau nhà khi chưa giảm giá là 200 nghìn đồng
Bài 4:
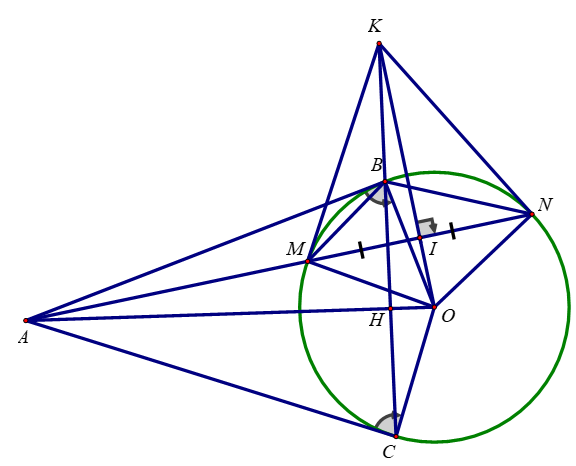
a) Ta có: ∠ABO = 90o(Do BA là tiếp tuyến của (O)) nên B thuộc đường tròn đường kính OA
Tương tự ∠ACO = 90onên C thuộc đường tròn đường kính OA
Do I là trung điểm của MN nên OI ⊥ MN
=> ∠AIO = 90o => I thuộc đường tròn đường kính OA
Vậy 5 điểm O, A , B, C, I cùng thuộc đường tròn đường kính OA
b) Xét ΔABM và ΔANB có:
∠BAN là góc chung
∠ABM = ∠ANB (2 góc cùng chắn ⏜BM)
=> ΔABM ∼ ΔANB
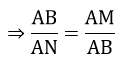
Xét tam giác OAB vuông tại O có:
AB2 = OA2 – OB2 = (3R)2 – R2 = 8R2
c) Gọi độ dài AM là x
=> AN = x + R√3
Theo câu b ta có:
AM. AN = 8R2
=> x(x + R√3) = 8R2 ⇔ x2 + xR√3 – 8R2 = 0
Δ = (R√3)2 – 4.(- 8R2 ) = 35R2 => √Δ = R√35
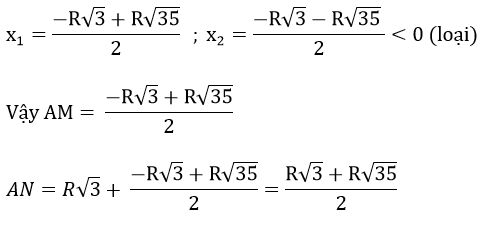
d) Ta có:
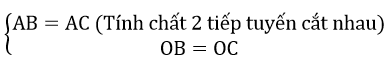 => AM.AN = AB2
=> AM.AN = AB2=> OA là đường trung trực của BC
Do đó OA ⊥ BC tại H
Xét ΔOHK và Δ OIA có:
∠AOK là góc chung
∠OHK = ∠OIA = 90o
=> ΔOHK ∼ ΔOIA
Mặt khác, xét tam giác ABO vuông tại B có BH là đường cao
=> OH.OA = OB2 = R2 (2)
Từ (1) và (2) => OK.OI = R2 = OM2
Xét tam giác OIM và tam giác OMK có:
∠MOK là góc chung
=> ΔOIM ∼ ΔOMK (c.g.c)
=> ∠OIM = ∠OMK = 90o Hay OM ⊥ MK
Vậy MK là tiếp tuyến của (O)
Chứng minh tương tự ta được NK là tiếp tuyến của (O).