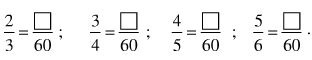Giải bài tập luyện tập trang 15, 16 SGK toán lớp 6 tập 2. Hướng dẫn làm bài tập 20, 21, 22, 23, 24, 25, 26, 27 trang 15, 16 SGK toán lớp 6 tập 2. Giải toán lớp 6 tập 2 trang 15, 16 SGK.
Tóm tắt nội dung
Giải bài tập luyện tập trang 15, 16 SGK toán lớp 6 tập 2
Bài 20 trang 15 SGK toán lớp 6 tập 2
Tìm các cặp phân số bằng nhau trong các phân số sau đây:
\[ \frac{-9}{33} \], \[ \frac{15}{9} \], \[ \frac{3}{-11} \], \[ \frac{-12}{19} \], \[ \frac{5}{3} \], \[ \frac{60}{-95} \].
Giải:
Cách chắc chắn nhất để tìm các phân số bằng nhau là ta rút gọn các phân số về phân số tối giản.
Ta có:
\[ \frac{-9}{33} = \frac{-3}{11}\];
\[ \frac{15}{9} = \frac{5}{3}\];
\[ \frac{60}{-95} = \frac{-12}{19} \].\[ \frac{-3}{11}\], \[ \frac{-12}{19} \], \[ \frac{5}{3} \] là những phân số tối giản.
Vậy trong các phân số đã cho, các phân số bằng nhau là:
\[ \frac{-9}{33} = \frac{3}{-11}\]; \[ \frac{15}{9} = \frac{5}{3}\]; \[ \frac{60}{-95} = \frac{-12}{19} \].
Bài 21 trang 15 SGK toán lớp 6 tập 2
Trong các phân số sau đây, tìm phân số không bằng phân số nào trong các phân số còn lại:
\[ \frac{-7}{42} \], \[ \frac{12}{18} \], \[ \frac{3}{-18} \], \[ \frac{-9}{54} \], \[ \frac{-10}{-15} \], \[ \frac{14}{20} \].
Giải:
Tương tự như bài 20, ta cũng rút gọn các phân số về phân số tối giản để so sánh.
Ta có:
\[ \frac{-7}{42} = \frac{-1}{6} \],
\[ \frac{12}{18} = \frac{2}{3} \],
\[ \frac{3}{-18} = \frac{1}{-6}\],
\[ \frac{-9}{54} = \frac{-1}{6}\],
\[ \frac{-10}{-15} = \frac{2}{3}\],
\[ \frac{14}{20} = \frac{7}{10}\].
Do đó: \[ \frac{-7}{42} = \frac{3}{-18} = \frac{-9}{54} \] (= \[ \frac{-1}{6} \]),
\[ \frac{-10}{-15} = \frac{12}{18} \] (=\[ \frac{2}{3}\],)
Vậy phân số phân số không bằng phân số nào trong các phân số còn lại là: \[ \frac{14}{20} \]
Bài 22 trang 15 SGK toán lớp 6 tập 2
Điền số thích hợp vào ô vuông:
Giải:
Gọi số cần tìm là x. Ta có:
– Trường hợp 1:
2.60 = 3.x x = 40.
– Trường hợp 2:
3.60 = 4.x x = 45.
– Trường hợp 3:
4.60 = 5.x x = 48.
– Trường hợp 4:
5.60 = 6.x x = 50.
Vậy điền vào ô vuông thứ tự lần lượt là: 40, 45, 48, 50.
Bài 23 trang 16 SGK toán lớp 6 tập 2
Cho tập hợp A = {0; -3; 5}. Viết tập hợp B các phân số m/n mà m, n ∈ A. (Nếu có hai phân số bằng nhau thì chỉ cần viết một phân số).
Giải:
Ta có: Mẫu số của một phân số phải khác 0 nên n 0.
Do đó m có thể chọn trong các số 0; -3; 5.
và n có thể chọn trong các số -3; 5.
Vậy ta có thể viết được các phân số \[ \frac{m}{n} \] là:
\[ \frac{0}{-3} \]; \[ \frac{0}{5} \]; \[ \frac{-3}{-3} \]; \[ \frac{-3}{-5} \]; \[ \frac{5}{-3} \]; \[ \frac{5}{5} \]
Tuy nhiên ta có \[ \frac{0}{-3} \] = \[ \frac{0}{5} \] = 0 và \[ \frac{-3}{-3} \] = \[ \frac{5}{5} \] = 1 nên theo đề bài ta chỉ cần viết một trong hai phân số.
Vậy B = \[ \{\frac{0}{-3}; \frac{-3}{-3}; \frac{-3}{-5} ; \frac{5}{-3} \} \]
Bài 24 trang 16 SGK toán lớp 6 tập 2
Tìm các số nguyên x và y, biết:
\[ \frac{3}{x} = \frac{y}{35} = \frac{-36}{84} \]Giải:
Ta có:
\[ \frac{-36}{84} = \frac{-3}{7} \]Vậy từ đề ra ta có:
\[ \frac{3}{x} = \frac{y}{35} = \frac{-3}{7} \]Từ: \[ \frac{3}{x} = \frac{-3}{7} \] =>3.7 = x.(-3) => x= -7
Từ: \[ \frac{y}{35} = \frac{-3}{7} \] => 7.y = 35.(-3) => y = -15
Vậy x = -7; y = -15.
Bài 25 trang 16 SGK toán lớp 6 tập 2
Viết tất cả các phân số bằng \[ \frac{15}{39} \] mà tử và mẫu là các số tự nhiên có hai chữ số.
Giải:
Trước tiên ta rút gọn phân số, ta có \[ \frac{15}{39} = \frac{5}{13}\]
Theo đề bài ta phải nhân cả tử và mẫu của phân số với cùng một số tự nhiên sao cho tử và mẫu của nó là các số tự nhiên có hai chữ số.
Ta có: \[ \frac{5}{13} = \frac{10}{26} = \frac{15}{39} = \frac{20}{52} = \frac{25}{65} = \frac{30}{78} = \frac{35}{91} = \frac{40}{104}\].
Vậy các phân số thỏa mãn yêu cầu của đề bài là \[ \frac{10}{26} \]; \[ \frac{20}{52} \]; \[ \frac{25}{65} \]; \[ \frac{30}{78} \]; \[ \frac{35}{91} \].
Bài 26 trang 16 SGK toán lớp 6 tập 2
Cho đoạn thẳng AB:
Hãy vẽ vào vở các đoạn thẳng CD, EF, GH, IK biết rằng:
CD = \[ \frac{3}{4} \] AB; EF = \[ \frac{5}{6} \] AB; GH = \[ \frac{1}{2} \] AB; IK = \[ \frac{5}{4} \] AB.
Giải:
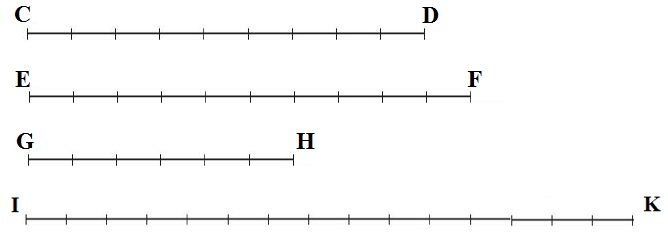
Ta có AB = 12 đơn vị.
Vậy CD = \[ \frac{3}{4} \] AB = 9 đơn vị.
EF = \[ \frac{5}{6} \] AB = 10 đơn vị.
GH = \[ \frac{1}{2} \] AB = 6 đơn vị.
IK = \[ \frac{5}{4} \] AB = 15 đơn vị.
Ta vẽ các đoạn thẳng như sau:
Bài 27 trang 16 SGK toán lớp 6 tập 2
Đố: Một học sinh đã rút gọn như sau:
\[ \frac{10 + 5}{10 + 10} = \frac{5}{10} = \frac{1}{2}\]Bạn đó giải thích: “Trước hết em rút gọn cho 10, rồi rút gọn cho 5”. Đố em làm như vậy đúng hay sai? Vì sao?
Giải:
Sai, ở biểu thức đầu tiên số 10 không phải là thừa số mà là số hạng (của tổng) nên không thể rút gọn cho 10 được. Ta phải phân tích tử số và mẫu số thành tích các thừa số mới rút gọn cho thừa số chung.
Rút gọn đúng như sau:
\[ \frac{10 + 5}{10 + 10} = \frac{15}{20} = \frac{5.3}{5.4} = \frac{3}{4}\]