Giải bài tập bài 11 trang 38, 39 SGK toán lớp 6 tập 2. Hướng dẫn giải bài tập về tính chất cơ bản của phép nhân phân số. Giải toán lớp 6 tập 2 bài 11 trang 38, 39 SGK.
Tóm tắt nội dung
Tính Chất Cơ Bản Của Phép Nhân Phân Số
1. Các tính chất của phép nhân phân số
– Tính chất giao hoán: \[\frac{a}{b}.\frac{c}{d} = \frac{c}{d}.\frac{a}{b}\]
– Tính chất kết hợp: \[(\frac{a}{b}.\frac{c}{d}).\frac{p}{q} = \frac{a}{b}.(\frac{c}{d}.\frac{p}{q})\]
– Nhân với số 1: \[\frac{a}{b}.1 = 1.\frac{a}{b}\] = \[\frac{a}{b}\]
– Nhân với số 0: \[\frac{a}{b}.1 = 1.\frac{a}{b}\].0 = 0
– Tính chất phân phối của phép nhân đối với phép cộng:
\[\frac{a}{b}.(\frac{c}{d} + \frac{p}{q}) = \frac{a}{b}.\frac{c}{d}+ \frac{a}{b}.\frac{p}{q}\]Nhận xét:
Lũy thừa của một phân số: Với n thừa số (n ∈ N):
2. Áp dụng tính chất của phép nhân phân số
Do tính chất giao hoán và kết hợp của phép nhân. Khi nhân nhiều số, ta có thể đổi chỗ hoặc nhóm các phân số lại theo bất cứ cách nào sao cho việc tính toán được thuận tiện.
Ví dụ: Tính:
A = \[\frac{2}{3}.\frac{7}{9}.\frac{3}{5}.\frac{9}{4}\]
= \[\frac{2}{3}.\frac{3}{5}.\frac{7}{9}.\frac{9}{4}\] (tính chất giao hoán)
= \[(\frac{2}{3}.\frac{3}{5}).(\frac{7}{9}.\frac{9}{4})\] (tính chất kết hợp)
= \[\frac{2}{5}.\frac{7}{4}\]
= \[\frac{7}{10}\]
Trả lời câu hỏi bài 11 trang 37 SGK toán lớp 6 tập 2
Câu hỏi 1 Bài 11 trang 37 Toán 6 Tập 2
Phép nhân số nguyên có những tính chất cơ bản gì?
Giải:
Phép nhân số nguyên có những tính chất:
– Tính chất giao hoán.
– Tính chất kết hợp.
– Nhân với số 1.
– Tính chất phân phối của phép nhân đối với phép cộng.
Câu hỏi 2 Bài 11 trang 38 Toán 6 Tập 2
Hãy vận dụng tính chất cơ bản của phép nhân để tính giá trị các biểu thức sau:
A = \[\frac{7}{11}.\frac{-3}{41}.\frac{11}{7}\]
B = \[\frac{-5}{9}.\frac{13}{28} – \frac{13}{28}.\frac{4}{9}\]
Giải:
A = \[\frac{7}{11}.\frac{-3}{41}.\frac{11}{7}\]
= \[\frac{7}{11}.\frac{11}{7}.\frac{-3}{41}\]
= \[\frac{-3}{41}\]
B = \[\frac{-5}{9}.\frac{13}{28} – \frac{13}{28}.\frac{4}{9}\]
= \[\frac{13}{28}.(\frac{-5}{9} – \frac{4}{9})\]
= \[\frac{13}{28}.\frac{-9}{9}\]
= \[\frac{13}{28}.(-1)\]
= \[\frac{-13}{28}.\]
Giải bài tập bài 11 trang 38 SGK toán lớp 6 tập 2
Bài 73 trang 38 SGK toán lớp 6 tập 2
Trong hai câu sau đây, câu nào đúng ?
Câu thứ nhất: Để nhân hai phân số cùng mẫu, ta nhân hai tử với nhau và giữ nguyên mẫu.
Câu thứ hai: Tích của hai phân số bất kì là một phân số có tử là tích của hai tử và mẫu là tích của hai mẫu.
Giải: Câu thứ hai đúng.
Bài 74 trang 39 SGK toán lớp 6 tập 2
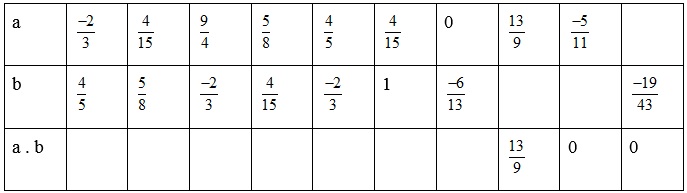
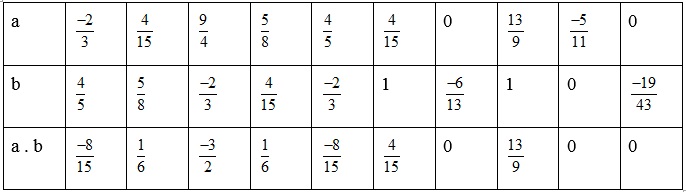
Điền các số thích hợp vào bảng sau:
Giải:
Thực hiện phép nhân và điền vào bảng. Ta có như sau:
Bài 75 trang 39 SGK toán lớp 6 tập 2
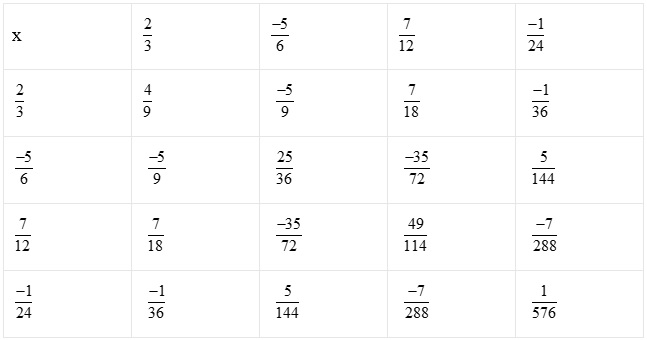
Hoàn thành bảng nhân sau (chú ý rút ngắn gọn nếu có thể):
Giải:
Thực hiện phép nhân và điền vào bảng. Ta có như sau:
Bài 76 trang 39 SGK toán lớp 6 tập 2
Tính giá trị biểu thức sau một cách hợp lí:
A = \[\frac{7}{19}.\frac{8}{11} + \frac{7}{19}.\frac{3}{11} + \frac{12}{19}\]
B = \[\frac{5}{9}.\frac{7}{13} + \frac{5}{9}.\frac{9}{13} – \frac{5}{9}.\frac{3}{13}\]
C = \[(\frac{67}{111} + \frac{2}{33} – \frac{15}{117}).(\frac{1}{3} – \frac{1}{4} – \frac{1}{12})\]
Giải:
A = \[\frac{7}{19}.\frac{8}{11} + \frac{7}{19}.\frac{3}{11} + \frac{12}{19}\]
= \[\frac{7}{19}.(\frac{8}{11} + \frac{3}{11}) + \frac{12}{19}\]
= \[\frac{7}{19}.1 + \frac{12}{19}\]
= 1
B = \[\frac{5}{9}.\frac{7}{13} + \frac{5}{9}.\frac{9}{13} – \frac{5}{9}.\frac{3}{13}\]
= \[\frac{5}{9}.(\frac{7}{13} + \frac{9}{13} – \frac{3}{13})\]
= \[\frac{5}{9}.1\]
= \[\frac{5}{9}\]
C = \[(\frac{67}{111} + \frac{2}{33} – \frac{15}{117}).(\frac{1}{3} – \frac{1}{4} – \frac{1}{12})\]
= \[(\frac{67}{111} + \frac{2}{33} – \frac{15}{117}).(\frac{4}{12} – \frac{3}{12} – \frac{1}{12})\]
= \[(\frac{67}{111} + \frac{2}{33} – \frac{15}{117}).0\]
= 0
Bài 77 trang 39 SGK toán lớp 6 tập 2
Tính giá trị các biểu thức sau:
A = \[a.\frac{1}{2} + a.\frac{1}{3} – a.\frac{1}{4}\] với \[a = \frac{-4}{5}\]
B = \[\frac{3}{4}.b + \frac{4}{3}.b – \frac{1}{2}.b\] với \[b = \frac{6}{19}\]
C = \[c.\frac{3}{4} + c.\frac{5}{6} – c.\frac{19}{12}\] với \[c = \frac{2002}{2003}\]
Giải:
Ta áp dụng tính chất phân phối của phép nhân đối với phép cộng rồi tính giá trị biểu thức sau hoặc thay giá trị vào biểu thức rồi thực hiện theo thứ tự thực hiện các phép tính.
Cách 1:
A = \[a.\frac{1}{2} + a.\frac{1}{3} – a.\frac{1}{4}\] với \[a = \frac{-4}{5}\]
= \[a.(\frac{6}{12} + \frac{4}{12} – \frac{3}{12})\]
= \[a.\frac{7}{12}\]
Với \[a = \frac{-4}{5}\] ta có:
A = \[\frac{-4}{5}.\frac{7}{12} = \frac{-7}{15}\]
Cách giải khác là thay giá trị của chữ vào biểu thức rồi thực hiện theo thứ tự thực hiện các phép tính.
Cách 2:
Thay \[a = \frac{-4}{5}\] vào biểu thức ta có:
A = \[\frac{-4}{5}.\frac{1}{2} + \frac{-4}{5}.\frac{1}{3} – \frac{-4}{5}.\frac{1}{4}\]
= \[\frac{-2}{5} + \frac{-4}{5} – \frac{-1}{5}\]
= \[– \frac{-7}{15}\]
Ở biểu thức B và C ta làm theo cách 1, các bạn có thể kiểm tra lại bằng cách 2 nhé.
B = \[\frac{3}{4}.b + \frac{4}{3}.b – \frac{1}{2}.b\]
= \[(\frac{3}{4} + \frac{4}{3} – \frac{1}{2}).b\]
= \[\frac{19}{12}.b\]
Với b = 6/19, ta có:
B = \[\frac{19}{12}.\frac{6}{19}\]
= \[\frac{1}{2}\]
C = \[c.\frac{3}{4} + c.\frac{5}{6} – c.\frac{19}{12}\]
= \[c.(\frac{3}{4} + \frac{5}{6} – \frac{19}{12})\]
= \[c.(\frac{9}{12} + \frac{10}{12} – \frac{19}{12})\]
= c. 0 = 0
Vậy với mọi giá trị của c (ở đây ta có c = 2002/2003), ta luôn có biểu thức C = 0.