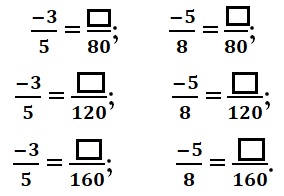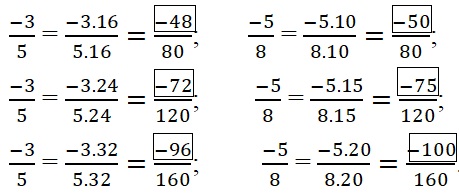Giải toán lớp 6 tập 2 bài 5: Quy Đồng Mẫu Nhiều Phân Số. Giải bài tập trang 19 SGK toán lớp 6 tập 2. Hướng dẫn giải bài tập 28, 29, 30, 31 trang 19 SGK toán lớp 6 tập 2.
Tóm tắt nội dung
Lý thuyết bài 5: Quy Đồng Mẫu Nhiều Phân Số
Quy đồng mẫu số của nhiều phân số là biến đổi những phân số đó lần lượt thành những phân số bằng chúng nhưng có cùng mẫu số với các phân số còn lại.
1. Quy đồng mẫu hai phân số
Muốn quy đồng hai phân số ta làm như sau:
Bước 1: Tìm một bội chung của 2 mẫu số để làm mẫu chung.
Bước 2: Tìm thừa số phụ của mỗi mẫu (chia mẫu chung cho từng mẫu).
Bước 3: Nhân cả tử và mẫu của mỗi phân số với thừa số phụ tương ứng.
Ví dụ: Quy đồng mẫu số hai phân số \[\frac{7}{11}\] và \[\frac{3}{2}\]
Giải: Ta có 22 là bội chung của 11 và 2
Vậy: \[\frac{7}{11} = \frac{7.2}{11.2} = \frac{14}{22}\] (thừa số phụ ở đây là 2)
\[\frac{3}{2} = \frac{3.11}{2.11} = \frac{33}{22}\] (thừa số phụ ở đây là 11)
Vậy hai phân số \[\frac{7}{11}\] và \[\frac{3}{2}\] được quy đồng mẫu số thành hai phân số tương ứng là \[\frac{14}{22}\] và \[\frac{33}{22}\].
2. Các bước quy đồng mẫu số nhiều phân số với mẫu số dương
Muốn quy đồng nhiều phân số với mẫu số dương ta làm như sau:
Bước 1: Tìm một bội chung của các mẫu (thường là BCNN) để là mẫu chung.
Bước 2: Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu).
Bước 3: Nhân cả tử và mẫu của mỗi phân số với thừa số phụ tương ứng.
Ví dụ: Quy đồng mẫu số của các phân số sau \[\frac{5}{6}\]; \[\frac{7}{11}\] và \[\frac{3}{2}\].
Giải: Ta có:
BCNN(6; 11; 2) = 66. Vậy mẫu chung của các phân số đã cho 66.
Ta có: \[\frac{5}{6} = \frac{5.11}{6.11} = \frac{55}{66}\] (thừa số phụ là 11);
\[\frac{7}{11} = \frac{7.6}{11.6} = \frac{42}{66}\] (thừa số phụ là 6)
\[\frac{3}{2} = \frac{3.33}{2.33} = \frac{99}{66}\] (thừa số phụ là 33).
Vậy 3 phân số \[\frac{5}{6}\]; \[\frac{7}{11}\] và \[\frac{3}{2}\] được quy đồng mẫu số thành 3 phân số tương ứng là \[\frac{55}{66}\]; \[\frac{42}{66}\] và \[\frac{99}{66}\].
Trả lời câu hỏi bài 5 trang 17 SGK toán lớp 6 tập 2
Câu hỏi 1 Bài 5 trang 17 Toán 6 Tập 2
Hãy điền số thích hợp vào ô vuông
Giải:
Ta có:
Câu hỏi 2 Bài 5 trang 17 Toán 6 Tập 2
a) Tìm BCNN của các số 2, 5, 3, 8.
b) Tìm các phân số lần lượt bằng \[\frac{1}{2}\]; \[\frac{-3}{5}\]; \[\frac{2}{3}\]; \[\frac{-5}{8}\] nhưng cùng có mẫu là BCNN(2, 5, 3, 8).
Giải:
a) Ta có 8 = 23
Các thừa số chung và riêng là 2; 3; 5.
Số mũ lớn nhất của 2 là 3.
Số mũ lớn nhất của 3 là 1.
Số mũ lớn nhất của 5 là 1
Khi đó: BCNN(2,5,3,8) = 23 . 3 . 5 = 120
b) Ta có các phân số lần lượt bằng \[\frac{1}{2}\]; \[\frac{-3}{5}\]; \[\frac{2}{3}\]; \[\frac{-5}{8}\] nhưng cùng có mẫu là BCNN(2,5,3,8) là quy đồng mẫu số các phân số \[\frac{1}{2}\]; \[\frac{-3}{5}\]; \[\frac{2}{3}\]; \[\frac{-5}{8}\] với mẫu chung là BCNN(2,5,3,8) = 120.
Ta có:
\[\frac{1}{2} = \frac{1.60}{2.60} = \frac{60}{120}\];
\[\frac{-3}{5} = \frac{-3.24}{5.24} = \frac{-72}{120}\]; \[\frac{2}{3} = \frac{2.40}{3.40} = \frac{80}{120}\]; \[\frac{-5}{8} = \frac{-5.15}{8.15} = \frac{-75}{120}\].Câu hỏi 3 Bài 5 trang 18 Toán 6 Tập 2
a) Điền vào chỗ trống để quy đồng mẫu các phân số: \[\frac{5}{12}\] và \[\frac{7}{30}\]
– Tìm BCNN(12, 30):
12 = 22 . 3
30 = …
BCNN(12, 30) = …
– Tìm thừa số phụ:
… : 12 = …
… : 30 = …
– Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng:
\[\frac{5}{12} = \frac{5…}{12…} = \frac{…}{…}\]; \[\frac{7}{30} = \frac{7…}{30…} = \frac{…}{…}\]b) Quy đồng mẫu các phân số: \[\frac{-3}{44}\]; \[\frac{-11}{18}\]; \[\frac{5}{-36}\].
Giải:
a) – Tìm BCNN(12,30)
12 = 22.3
30 = 2 . 3 . 5
BCNN(12,30) = 22.3.5 = 60
– Tìm thừa số phụ:
60 : 12 = 5
60 : 30 = 2
– Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng:
\[\frac{5}{12} = \frac{5.5}{12.5} = \frac{25}{60}\]; \[\frac{7}{30} = \frac{7.2}{30.2} = \frac{14}{60}\]b) Ta có:
44 = 22.11
18 = 2.32
36 = 22.32
BCNN(44,8,36) = 22.32.11 = 396
– Thừa số phụ:
396 : 44 = 9
396 : 18 = 22
396 : (-36) = -11
– Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng ta được kết quả như sau:
\[\frac{-3}{44} = \frac{-3.9}{44.9} = \frac{-27}{396}\];
\[\frac{-11}{18} = \frac{-11.22}{18.22} = \frac{-242}{396}\];
\[\frac{5}{-36} = \frac{5.(-11)}{-36.(-11)} = \frac{-55}{396}\].
Giải bài tập bài 5 trang 19 SGK toán lớp 6 tập 2
Bài 28 trang 19 SGK toán lớp 6 tập 2
a) Quy đồng mẫu các phân số sau: \[\frac{-3}{16}\]; \[\frac{5}{24}\]; \[\frac{-21}{56}\].
b) Trong các phân số đã cho, phân số nào chưa tối giản?
Từ nhận xét đó, ta có thể quy đồng các phân số này như thế nào?
Giải:
a) Ta có: Mẫu số chung là BCNN(16, 24, 56) = 24.3.7 = 336
Quy đồng mẫu:
\[\frac{-3}{16} = \frac{-3.21}{16.21} = \frac{-63}{336}\] (thừa số phụ là 21);
\[\frac{5}{24} = \frac{5.14}{24.14} = \frac{70}{336}\] (thừa số phụ là 14);
\[\frac{-21}{56} = \frac{-21.6}{56.6} = \frac{-126}{336}\] (thừa số phụ là 6).
b) Ta có phân số \[\frac{-21}{56}\] không phải là phân số tối giản.
Từ đó ta có thể quy đồng mẫu các phân số đã cho, trước hết nên rút gọn các phân số đã cho thành phân số tối giản rồi hãy quy đồng mẫu.
Ta có: \[\frac{-21}{56} = \frac{-3}{8}\]
Mẫu chung của \[\frac{-3}{16}\]; \[\frac{5}{24}\] và \[\frac{-3}{8}\] là 48.
Sau khi quy đồng mẫu ta được kết quả đơn giản hơn là \[\frac{-9}{48}\]; \[\frac{10}{48}\] và \[\frac{-18}{48}\]
Bài 29 trang 19 SGK toán lớp 6 tập 2
Quy đồng mẫu các phân số sau:
a) \[\frac{3}{8}\] và \[\frac{5}{27}\]
b) \[\frac{-2}{9}\] và \[\frac{4}{25}\]
c) \[\frac{1}{15}\] và -6
Giải:
a) Ta có mẫu chung là BCNN(8,27) = 8.27 = 216
Vậy \[\frac{3}{8} = \frac{3.27}{8.27}\] = \[\frac{81}{216}\];
\[\frac{5}{27}\] = \[\frac{5.8}{27.8}\] = \[\frac{40}{216}\].b) Ta có mẫu chung là BCNN(9,25) = 9.25 = 225
Vậy \[\frac{-2}{9}\] = \[\frac{-2.25}{9.25}\] = \[\frac{-50}{225}\];
\[\frac{4}{25}\] = \[\frac{4.9}{25.9}\] = \[\frac{36}{225}\]c) Ta có -6 = \[\frac{-6}{1}\] nên mẫu chung của \[\frac{1}{15}\] và -6 là 15
Vậy \[\frac{1}{15}\] và -6 quy đồng mẫu sẽ là \[\frac{1}{15}\] và -6 = \[\frac{-6.15}{15}\] = \[\frac{-90}{15}\].
Bài 30 trang 19 SGK toán lớp 6 tập 2
Quy đồng mẫu các phân số sau:
a) \[\frac{11}{120}\] và \[\frac{7}{40}\];
b) \[\frac{24}{146}\] và \[\frac{6}{13}\];
c) \[\frac{7}{30}\], \[\frac{13}{60}\], \[\frac{-9}{40}\]
d) \[\frac{17}{60}\], \[\frac{-5}{18}\], \[\frac{-64}{90}\]
Giải:
a) Ta có mẫu chung là BCNN(120,40) = 120.
Vậy quy đồng mẫu \[\frac{11}{120}\] và \[\frac{7}{40}\] ta được \[\frac{11}{120}\] và \[\frac{7}{40}\] = \[\frac{7.3}{40.3}\] = \[\frac{21}{120}\]
b) Rút gọn \[\frac{24}{146}\] ta được \[\frac{24}{146}\] = \[\frac{12}{73}\]
Ta có mẫu chung của \[\frac{24}{146}\] và \[\frac{6}{13}\] là BCNN(73,13) = 73.13 = 949
Vậy quy đồng mẫu như sau:
\[\frac{24}{146}\] = \[\frac{12}{73}\] = \[\frac{12.13}{73.13}\] = \[\frac{156}{949}\]\[\frac{6}{13}\] = \[\frac{6.73}{13.73}\] = \[\frac{438}{949}\]
c) Ta có mẫu số chung là BCNN(30,60,40) = 120.
Vậy quy đồng mẫu số ta được
\[\frac{7}{30}\] = \[\frac{7.4}{30.4}\] = \[\frac{28}{120}\],
\[\frac{13}{60}\] = \[\frac{13.2}{60.2}\] = \[\frac{26}{120}\],
\[\frac{-9}{40}\] = \[\frac{-9.3}{40.3}\] = \[\frac{-27}{120}\].d) Ta có mẫu số chung là BCNN(60,18,90) = 180
Vậy quy đồng mẫu số ta được:
\[\frac{17}{60} = \frac{17.3}{60.3} = \frac{51}{180}\],
\[\frac{-5}{18} = \frac{-5.10}{18.10} = \frac{-50}{180}\], \[\frac{-64}{90} = \frac{-64.2}{90.2} = \frac{-128}{180}\].Bài 31 trang 19 SGK toán lớp 6 tập 2
Hai phân số sau đây có bằng nhau không?
a) \[\frac{-5}{14}\] và \[\frac{30}{-84}\]
b) \[\frac{-6}{102}\] và \[\frac{-9}{153}\]
Giải:
a) Rút gọn phân số \[\frac{30}{-84}\]. Ta chia cả tử và mẫu cho -6 ta được:
\[\frac{30}{-84}\] = \[\frac{30:(-6)}{-84:(-6)}\] = \[\frac{-5}{14}\]Vậy hai phân số đã cho bằng nhau.
b) Rút gọn cả hai phân số. Ta có:
Chia cả tử và mẫu phân số \[\frac{-6}{102}\] với 2, ta được:
\[\frac{-6}{102}\] = \[\frac{-6:2}{102:2}\] = \[\frac{-3}{51}\]Chia cả tử và mẫu phân số \[\frac{-9}{153}\] với 3, ta được:
\[\frac{-9}{153}\] = \[\frac{-9:3}{153:3}\] = \[\frac{-3}{51}\]Vậy hai phân số đã cho bằng nhau.