Giải bài tập vẽ đoạn thẳng cho biết độ dài toán lớp 6 bài 9 trang 124 SGK. Hướng dẫn giải toán lớp 6 bài 9 trang 124 SGK. Giải các bài tập 53, 54, 55, 56, 57, 58, 59 SGK toán lớp 6 tập 1.
Tóm tắt nội dung
Lý thuyết bài 9: Vẽ đoạn thẳng cho biết độ dài
1. Vẽ đoạn thẳng trên tia
Cách 1: Dùng thước đo có chia khoảng (tương tự như đo đoạn thẳng).
Cách 2: Dùng compa.
Nhận xét: Trên tia Ox bao giờ cũng vẽ được một và chỉ một điểm M sao cho OM = a (đơn vị độ dài).
2. Dấu hiệu nhận biết một điểm nằm giữa hai điểm khác
Trên tia Ox có hai điểm M và N, OM = a, ON = B, a < b thì điểm M nằm giữa hai điểm O và N.
Khi đó: ON = ON + MN
Giải bài tập bài 9 trang 124 SGK toán lớp 6 tập 1
Bài 53 trang 124 SGK toán lớp 6
Trên tia Ox, vẽ hai đoạn thẳng OM và ON sao cho OM = 3cm, ON = 6cm. Tính MN, so sánh OM và MN.
Giải:
Trên tia Ox ta có 2 điểm M, N mà OM < ON (3<6) nên điểm M nằm giữa hai điểm O và N.
Suy ra OM + MN = ON;
MN = ON – OM = 6 – 3 = 3(cm).
Vậy OM = MN = 3 (cm).
Bài 54 trang 124 SGK toán lớp 6
Trên tia Ox, vẽ ba đoạn thẳng OA, OB, OC sao cho OA = 2cm , OB = 5cm, OC = 8 cm. So sánh BC và BA.
Giải:

Ta có:
OC = 8cm; OB = 5 cm
=> OB < OC (5cm < 8 cm)
Do đó điểm B nằm giữa O và C, ta có
OB + BC = OC
=> 5 + BC = 8
=> BC = 8 – 5 = 3 (cm)
Ta có:
OA = 2cm; OB = 5cm
=> OA < OB (2cm < 5cm)
Do đó điểm A nằm giữa hai điểm O và B, ta có
OA + AB = OB
=> 2 + AB = 5
=> AB = 5 – 2 = 3 (cm)
Vậy AB = BC (=3cm)
Bài 55 trang 124 SGK toán lớp 6
Gọi A, B là hai điểm trên tia Ox. Biết OA= 8cm, AB= 2cm. Tình OB. Bài toán có mấy đáp số.
Giải:
Có hai trường hợp xảy ra:
Trường hợp 1: Điểm B và O nằm cùng phía với A
Do điểm B và O nằm cùng phía với A nên điểm B nằm giữa hai điểm A và O
Ta có: AB + BO = AO
=> 2 + OB = 8
=> OB = 8 – 2 = 6 (cm)
Vậy: OB = 6 (cm)
Trường hợp 2: Điểm B và O nằm khác phía đối với điểm A
Do điểm B và điểm O nằm về 2 phía đối với điểm A nên điểm A nằm giữa 2 điểm B và O.
Ta có OA + AB = OB
=> OB = 8 + 2 = 10 (cm)
Vậy OB = 10 (cm)
Kết luận: Bài toán có hai đáp số là 6 cm và 10 cm.
Bài 56 trang 124 SGK toán lớp 6
Cho đoạn thẳng AB dài 4 cm. Trên tia AB lấy điểm C sao cho AC =1 cm.
a) Tính CB
b) Lấy điểm D thuộc tia đối của tia BC sao cho BD=2cm. Tính CD.
Giải:
a) Trên tia AB có hai điểm C, B mà AC< AB (1cm<4cm) nên C nằm giữa hai điểm A và B.
Ta có:
AC+ CB = AB
⇒ 1+ CB = 4
⇒ CB = 3(cm)
b) Điểm D thuộc tia đối của tia BC nên điểm B nằm giữa C và D.
Ta có: CD = CB + BD = 3 + 2 = 5(cm)
Bài 57 trang 124 SGK toán lớp 6
Đoạn thẳng AC dài 5cm. Điểm B nằm giữa A và C sao cho BC= 3cm.
a) Tính AB.
b) Trên tia đối của tia BA lấy điểm D sao cho BD= 5cm. so sánh AB và CD.
Giải:
a) Điểm B nằm giữa A và C nên AB + BC = AC;
=> AB = AC – BC = 5 – 3 = 2 (cm).
b) Hai tia BC và BD trùng nhau (vì đều là tia đối của tia BA). Trên tia BC có BC< BD (3<5) nên C nằm giữa B và D.
Suy ra BC + CD = BD
=> CD = BD – BC = 5 – 3 = 2(cm).
Vậy AB = CD (= 2cm).
Bài 58 trang 124 SGK toán lớp 6
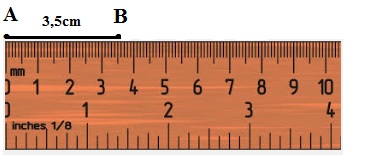
Vẽ đoạn thẳng AB dài 3,5 cm và nói cách vẽ.
Giải:
* Cách 1:
B1: Lấy điểm A bất kì trên mặt phẳng giấy.
B2: Đặt thước sao cho vạch số 0 trùng với điểm A. Tại vạch 3,5cm đánh dấu điểm B.
B3: Nối đoạn thẳng AB ta được đoạn AB = 3,5cm cần vẽ.
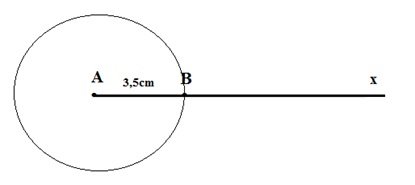
* Cách 2:
B1: Vẽ tia Ax.
B2: Dùng Compa vẽ đường tròn tâm là A bán kính 3,5cm, quay một vòng.
B3: Đường tròn cắt tia Ax tại B. Như vậy ta được đoạn thẳng AB = 3,5 cm.
Bài 59 trang 124 SGK toán lớp 6
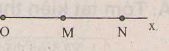
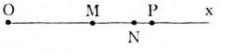
Trên tia Ox, cho ba điểm M, N, P biết OM = 2cm, ON = 3cm, OP = 3,5 cm. Hỏi trong ba điểm M, N, P thì điểm nào nằm giữa hai điểm còn lại? Vì sao?
Giải:
– Trên tia Ox có OM < OP (2 cm < 3,5 cm) nên M nằm giữa O và P. Ta có: OP = OM + MP (1)
– Trên tia Ox có ON < OP (3cm < 3,5 cm) nên N nằm giữa O và P. Ta có: OP = ON + NP (2)
Từ (1) và (2), ta có:
OM + MP = ON + NP.
Ta cũng có trên tia Ox có OM < ON (2 cm < 3 cm) nên điểm M nằm giữa O và N. Nên ON = OM + MN.
Vậy: OM + MP = ON + NP = OM + MN + NP
=> MP = MN + NP
Do đó điểm N nằm giữa hai điểm M và P.
Lưu ý: Nếu trên tia Ox có 3 điểm M, N, P; OM = a; ON = b; OP = c nếu a<b<c thì ta sẽ có điểm N nằm giữa hai điểm M và P. Cách chứng minh tương tự như bài giải phía trên.