Giải toán lớp 6 tập 2 trang 5 bài 1 với nội dung là mở rộng khái niệm phân số. Giải bài tập 1, 2, 3, 4, 5 trang 5 SGK toán lớp 6 tập 2.
Tóm tắt nội dung
Lý thuyết bài 1: Mở rộng khía niệm phân số
1. Khái niệm về phân số
Người ta gọi \[ \frac {a}{b} \] với a, b ∈ Z; b ≠ 0 là một phân số, a là tử số (tử), b là mẫu số (mẫu) của phân số.
Chú ý:
– Mọi số nguyên a có thể viết dưới dạng phân số là \[ \frac {a}{1} \].
– Phân số âm: là phân số có tử và mẫu là các số nguyên khác dấu.
– Phân số dương: là phân số có tử và mẫu là các số nguyên cùng dấu.
2. Ví dụ về phân số
Ví dụ: Các phân số như: \[ \frac {2}{3} \]; \[ \frac {-3}{5} \]; \[ \frac {6}{10} \]; \[ \frac {-1}{-9} \]…
Trả lời câu hỏi toán lớp 6 tập 2 trang 5 SGK
Câu hỏi 1 Bài 1 trang 5 SGK Toán 6 Tập 2
Cho ba ví dụ về phân số. Cho biết tử và mẫu của mỗi phân số đó.
Giải:
Các bạn có thể lấy rất nhiều ví dụ về phân số, ở đây mình lấy 3 ví dụ trong phần ví dụ phía trên và nói về tử, mẫu của nó.
– Phân số \[ \frac {-3}{5} \], có -3 là tử số, 5 là mẫu số.
– Phân số \[ \frac {-1}{-9} \], có -1 là tử số, -9 là mẫu số.
– Phân số \[ \frac {2}{3} \], có 2 là tử số, 3 là mẫu số.
Câu hỏi 2 Bài 1 trang 5 SGK Toán 6 Tập 2
Trong các cách viết sau đây, cách viết nào cho ta phân số?
a) \[ \frac {4}{7} \] b) \[ \frac {0,25}{-3} \] c) \[ \frac {-2}{3} \]
d) \[ \frac {6,23}{7,4} \] e) \[ \frac {3}{0} \]
Giải:
Cách viết cho ta phân số là a, c.
Cách viết b, d có tử số (câu d là cả mẫu số) là số thập phân (không thuộc Z) nên không cho ta phân số.
Cách viết e có mẫu số bằng 0 nên không cho ta phân số.
Câu hỏi 3 Bài 1 trang 5 Toán 6 Tập 2
Mọi số nguyên có thể viết dưới dạng phân số không? Cho ví dụ.
Giải
Mọi số nguyên có thể viết được dưới dạng phân số là đúng.
Ví dụ: Số 0 có thể viết dưới dạng phân số là \[ \frac {0}{1} \]
Số 11 có thể viết dưới dạng phân số là \[ \frac {11}{1} \]
Giải bài tập toán lớp 6 tập 2 trang 5
Bài 1 trang 5 SGK toán lớp 6 tập 2
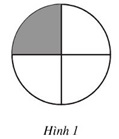
Ta biểu diễn 1/4 của hình tròn bằng cách chia hình tròn bằng 4 phần bằng nhau rồi tô màu một phần như hình 1.
Theo đó hãy biểu diễn:
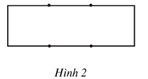
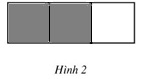
a) 2/3 của hình chữ nhật (h.2).
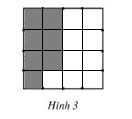
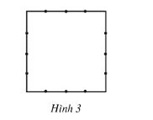
b) 7/16 của hình vuông (h.3).
Giải:
a) 2/3 của hình chữ nhật: Các bạn có 3 cách tô, tức là tô hai ô trong số 3 ô là được, ở đây là 1 cách.
b) 7/16 của hình vuông: Có rất nhiều cách tô khác nhau, đảm bảo tô 7 ô trong số 16 ô mà ta đã chia ra bằng nhau là được, dưới đây là 1 cách tô.
Bài 2 trang 6 SGK toán lớp 6 tập 2
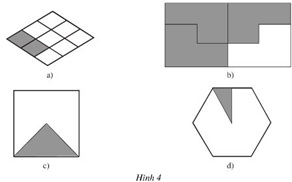
Phần tô màu trong các hình 4a, b, c, d biểu diễn phân số nào?
Giải:
Hình 4a và 4b đã rõ ràng, còn lại hình 4c và 4d chúng ta phải chia các hình ra thành các phần bằng nhau, để xem phần tô màu chiếm mấy phần trong hình đó. Ta chia như sau:
a) Hình a biểu diễn phân số: \[ \frac {2}{9} \]
b) Hình b biểu diễn phân số: \[ \frac {3}{4} \]
c) Hình c biểu diễn phân số: \[ \frac {1}{4} \]
d) Hình c biểu diễn phân số: \[ \frac {1}{12} \]
Lưu ý: ở hình 4b ta cũng có thể chia thành các hình chữ nhật nhỏ như sau:
Và như vậy hình 4b sẽ biểu diễn phân số \[ \frac {9}{12} \]
Ở các bài sau chúng ta sẽ học rút gọn phân số, ta có \[ \frac {9}{12} = \frac {3}{4} \]; \[ \frac {3}{4} \] gọi là phân số tối giản.
Bài 3 trang 6 SGK toán lớp 6 tập 2
Viết các phân số sau:
a) Hai phần bảy ; b) Âm năm phần chín ;
c) Mười một phần mười ba ; c) Mười bốn phần năm.
Giải:
a) Hai phần bảy: \[ \frac {2}{7} \];
b) Âm năm phần chín: \[ \frac {-5}{9} \];
c) Mười một phần mười ba: \[ \frac {11}{13} \];
c) Mười bốn phần năm: \[ \frac {14}{100} \] (còn được ký hiệu là 14%).
Bài 4 trang 6 SGK toán lớp 6 tập 2
Viết các phép chia sau dưới dạng phân số.
a) 3 : 11 ; b) -4 : 7
c) 5 : (-13) d) x chia cho 3 (x ∈ Z).
Giải:
a) 3 : 11 viết là: \[ \frac {3}{11} \]; b) -4 : 7 viết là: \[ \frac {-4}{7} \]
c) 5 : (-13) viết là: \[ \frac {5}{-13} \]
d) x chia cho 3 (x ∈ Z) viết là: \[ \frac {x}{3} \].
Bài 5 trang 6 SGK toán lớp 6 tập 2
Dùng cả hai số 5 và 7 để viết thành phân số, mỗi số chỉ được viết một lần. Cũng hỏi như vậy với hai số 0 và -2.
Giải:
Dùng cả hai số 5 và 7 để viết thành phân số. Ta được 2 phân số là:
\[ \frac {5}{7} \] và \[ \frac {7}{5} \]
Dùng hai số 0 và -2 để viết thành phân số. Ta viết được 1 phân số, vì mẫu số không thể bằng 0, nên phân số viết được là: \[ \frac {0}{-2} \]