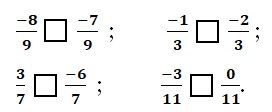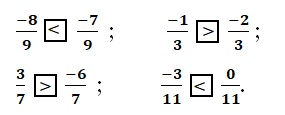Giải toán lớp 6 tập 2 trang 23, 24 về nội dung so sánh phân số. Hướng dẫn làm bài tập 37, 38, 39, 40, 41 trang 23, 24 SGK toán lớp 6 tập 2.
Tóm tắt nội dung
Lý thuyết về So Sánh Phân Số
1. So sánh hai phân số cùng mẫu
Trong hai phân số có cùng một mẫu dương, phân số nào có tử lớn hơn thì lớn hơn.
Ví dụ: \[ \frac{-6}{10}\] > \[ \frac{-9}{10}\] vì -6 > -9
2. So sánh hai phân số không cùng mẫu
Muốn so sánh hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi so sánh các tử với nhau: phân số nào có tử lớn hơn thì lớn hơn.
3. Nhận xét
– Phân số có tử và mẫu là hai số nguyên cùng dấu thì lớn hơn 0, gọi là phân số dương
Ví dụ: \[ \frac{-5}{-8}\] > 0; \[ \frac{4}{9}\] > 0
– Phân số có tử và mẫu là hai số nguyên khác dấu thì nhỏ hơn 0, gọi là phân số âm
Ví dụ: \[ \frac{-2}{7}\] < 0
– Ta còn có cách so sánh phân số như sau:
+ Áp dụng tính chất:
\[ \frac{a}{b}\] > \[ \frac{c}{d}\] <=> a.d = b.c (\[a,b,c,d \in Z\], b,d > 0)+ Đưa về hai phân số có cùng tử dương rồi so sánh mẫu. Phân số nào có mẫu nhỏ hơn thì lớn hơn (chỉ áp dụng với các phân số cùng dấu)
Ví dụ:
\[ \frac{5}{-3}\] > \[ \frac{5}{-2}\]; \[ \frac{8}{11}\] < \[ \frac{8}{9}\]+ Chọn số thứ ba làm trung gian:
Ví dụ:
\[ \frac{-2}{3} < 0 < \frac{1}{11}\]; \[ \frac{1}{11} < 1 < \frac{9}{8}\].Trả lời câu hỏi bài 6 trang 22 SGK toán lớp 6 tập 2
Câu hỏi 1 Bài 6 trang 22 Toán 6 Tập 2
Điền dấu thích hợp (< , >) vào ô vuông:
Giải:
Câu hỏi 2 Bài 6 trang 23 Toán 6 Tập 2
So sánh các phân số:
a) \[ \frac{-11}{12}\] và \[ \frac{17}{-18}\]
b) \[ \frac{-14}{21}\] và \[ \frac{-60}{-72}\]
Giải:
a) Quy đồng mẫu số hai phân số đã cho, ta có
Mẫu số chung là BCNN(12; 18) = 36.
Vậy:
\[ \frac{-11}{12} = \frac{-11.3}{12.3} = \frac{-33}{36}\] \[ \frac{17}{-18} = \frac{17.(-2)}{-18.(-2)} = \frac{-34}{36}\]
Vì -33 > -34 nên \[ \frac{-33}{34} > \frac{-34}{36} \]
Vậy \[ \frac{-11}{12} > \frac{17}{-18} \]
b) Ta có: \[ \frac{-14}{21} < 0 < \frac{-60}{-72} \]
Vậy \[ \frac{-14}{21} < \frac{-60}{-72} \]
Câu hỏi 3 Bài 6 trang 23 Toán 6 Tập 2
So sánh các phân số sau với 0:
\[ \frac{3}{5}\]; \[ \frac{-2}{-3}\]; \[ \frac{-3}{5}\]; \[ \frac{2}{-7}\].Giải:
\[ \frac{3}{5} > 0\]; \[ \frac{-2}{-3} > 0\]; \[ \frac{-3}{5} < 0\]; \[ \frac{2}{-7} < 0\].Giải bài tập bài 6 trang 23 SGK toán lớp 6 tập 2
Bài 37 trang 23 SGK toán lớp 6 tập 2
Điền số thích hợp vào chỗ chấm.
a) \[ \frac{-11}{13} < \frac{…}{13} < \frac{…}{13} < \frac{…}{13} < \frac{-7}{13} \]
b) \[ \frac{-1}{3} < \frac{…}{36} < \frac{…}{18} < \frac{-1}{4} \]
Giải:
a) Ta có các số liền nhau liên tiếp như sau -11 < -10 < -9 < -8 < -7 nên ta điền vào chỗ chấm đã cho là:
\[ \frac{-11}{13} < \frac{-10}{13} < \frac{-9}{13} < \frac{-8}{13} < \frac{-7}{13} \]b) Quy đồng mẫu các phân số ta được:
\[ \frac{-12}{36} < \frac{…}{36} < \frac{…}{36} < \frac{-9}{36} \]Ta có các số liền nhau liên tiếp -12 < -11 < -10 < -9 nên ta có:
\[ \frac{-12}{36} < \frac{-11}{36} < \frac{-10}{36} < \frac{-9}{36} \]Vậy điền vào chỗ chấm như sau:
\[ \frac{-1}{3} < \frac{-11}{36} < \frac{-5}{18} < \frac{-1}{4} \]Bài 38 trang 23-24 SGK toán lớp 6 tập 2
a) Thời gian nào dài hơn: \[ \frac{2}{3} \] h hay \[ \frac{3}{4} \] h?
b) Đoạn thẳng nào ngắn hơn: \[ \frac{7}{10} \] m hay \[ \frac{3}{4} \] m?
c) Khối lượng nào lớn hơn: \[ \frac{7}{8} \] kg hay \[ \frac{9}{10} \] kg?
d) Vận tốc nào nhỏ hơn: \[ \frac{5}{6} \] km/h hay \[ \frac{7}{9} \] km/h?
Giải:
Quy đồng mẫu số các phân số rồi so sánh ta có như sau:
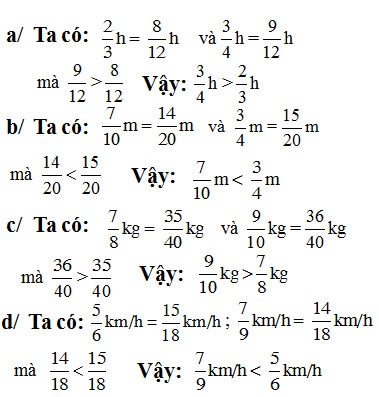
Bài 39 trang 24 Toán 6 tập 2
Lớp 6B có \[ \frac{4}{5} \] số học sinh thích bóng bàn, \[ \frac{7}{10} \] số học sinh thích bóng chuyền, \[ \frac{23}{25} \] số học sinh thích bóng đá. Môn bóng nào được nhiều bạn học sinh lớp 6B yêu thích nhất?
Giải:
Để biết môn bóng nào được nhiều bạn học sinh lớp 6B yêu thích nhất ta so sánh các phân số: \[ \frac{4}{5} \]; \[ \frac{7}{10} \] và \[ \frac{23}{25} \] xem số nào lớn nhất.
Quy đồng mẫu 3 phân số trên, ta có \[ \frac{4}{5} = \frac{40}{50} \]; \[ \frac{7}{10} = \frac{35}{50} \] và \[ \frac{23}{25} = \frac{46}{50} \]
Mà \[ \frac{35}{50} < \frac{40}{50} < \frac{46}{50}\] nên \[ \frac{7}{10} < \frac{4}{5} < \frac{23}{25} \]
Vậy \[ \frac{23}{25} \] lớn nhất.
Suy ra môn bóng đá được nhiều học sinh lớp 6B yêu thích nhất.
Bài 40 trang 24 SGK toán lớp 6 tập 2
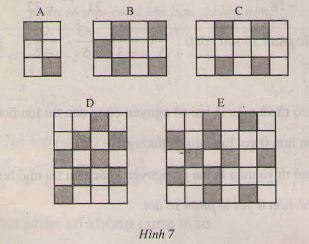
Lưới nào sẫm nhất?
a) Đối với mỗi lưới ô vuông hình 7, hãy lập một phân số có tử số là ô đen, mẫu số là tổng số ô đen và ô trắng.
b) Sắp xếp các phân số này theo thứ tự tăng dần và cho biết lưới nào sẫm nhất (có tỉ số ô đen so với tổng số ô là lớn nhất).
Giải:
Ta có thể lập các phân số rồi quy đồng mẫu các phân số vừa tìm được. Cũng có thể so sánh một số phân số đơn giản hơn với nhau rồi chọn phân số lớn nhất trong chúng để so sánh với những phân số còn lại.
a) Ta lập phân số tương ứng với các lưới ô vuông trong hình 7 như sau:
A tương ứng phân số \[ \frac{2}{6} \]
B tương ứng với phân số \[ \frac{5}{12} \]
C tương ứng với phân số \[ \frac{4}{15} \]
D tương ứng với phân số \[ \frac{8}{20} \]
E tương ứng với phân số \[ \frac{11}{30} \]
b) Sắp xếp các phân số theo thứ tự tăng dần:
Quy đồng mẫu các phân số trên với mẫu chung là 60 ta có:
\[ \frac{2}{6} = \frac{2.10}{6.10} = \frac{20}{60}\] \[ \frac{5}{12} = \frac{5.5}{12.5} = \frac{25}{60}\] \[ \frac{4}{15} = \frac{4.4}{15.4} = \frac{16}{60}\] \[ \frac{8}{20} = \frac{8.3}{20.3} = \frac{24}{60} \] \[ \frac{11}{30} = \frac{11.2}{30.2} = \frac{22}{60}\]Vì \[ \frac{16}{60} < \frac{20}{60} < \frac{22}{60} < \frac{24}{60} < \frac{25}{60} \] nên ta có \[ \frac{4}{15} < \frac{2}{6} < \frac{11}{30} < \frac{8}{20} < \frac{5}{12}\].
Vậy lưới B là lưới sẫm nhất.
Bài 41 trang 24 SGK toán lớp 6 tập 2
Đối với phân số ta có tính chất: Nếu \[ \frac{a}{b} > \frac{c}{d} \] và \[ \frac{c}{d} > \frac{p}{q}\] thì \[ \frac{a}{b} > \frac{p}{q} \] .
Dựa vào tính chất này, hãy so sánh:
a) \[ \frac{6}{7} \] và \[ \frac{11}{10} \]
b) \[ \frac{-5}{17} \] và \[ \frac{2}{7} \]
c) \[ \frac{419}{-723} \] và \[ \frac{-697}{-313} \]
Giải:
a) Ta có \[ \frac{6}{7} \] < 1 < \[ \frac{11}{10} \]
Vậy \[ \frac{6}{7} \] < \[ \frac{11}{10} \]
b) Ta có \[ \frac{-5}{17} \] < 0 < \[ \frac{2}{7} \]
Vậy \[ \frac{-5}{17} \] < \[ \frac{2}{7} \]
c) Ta có \[ \frac{419}{-723} \] < 0 < \[ \frac{-697}{-313} \]
Vậy \[ \frac{419}{-723} \] < \[ \frac{-697}{-313} \]