Giải bài tập toán lớp 6 bài 14 trang 47 SGK. Số nguyên tố là gì, cách tìm số nguyên tố, số nguyên tố nhỏ nhất, hợp số là gì, hơp số nhỏ nhất, bảng số nguyên tố nhỏ hơn 1000.
Tóm tắt nội dung
Lý thuyết về số nguyên tố, hợp số và bảng số nguyên tố
1. Định nghĩa số nguyên tố là gì?
Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
Ví dụ: Ư(13) = {1; 13} nên 13 là số nguyên tố.
Cách kiểm tra một số là số nguyên tố: Để kết luận số a là số nguyên tố (a > 1), chỉ cần chứng tỏ rằng nó không chia hết cho mọi số nguyên tố mà bình phương không vượt quá a. (Các bạn có thể tự suy nghĩ lý do nhé, hoặc có thể comment tôi sẽ giải thích).
2. Định nghĩa hợp số là gì?
Hợp số là một số tự nhiên lớn hơn 1, có nhiều hơn hai ước.
Ví dụ: Số 15 có 4 ước là 1; 3; 5; 15 nên 15 là hợp số.
Lưu ý:
a) Số 0 và số 1 không phải là số nguyên tố cũng không phải là hợp số.
b) Số 2 là số nguyên tố nhỏ nhất và cũng là số nguyên tố chẵn duy nhất. Như vậy, trừ số 2, mọi số nguyên tố đều là số lẻ. Nhưng ngược lại, một số lẻ chưa chắc là số nguyên tố.
c) Có vô số số nguyên tố.
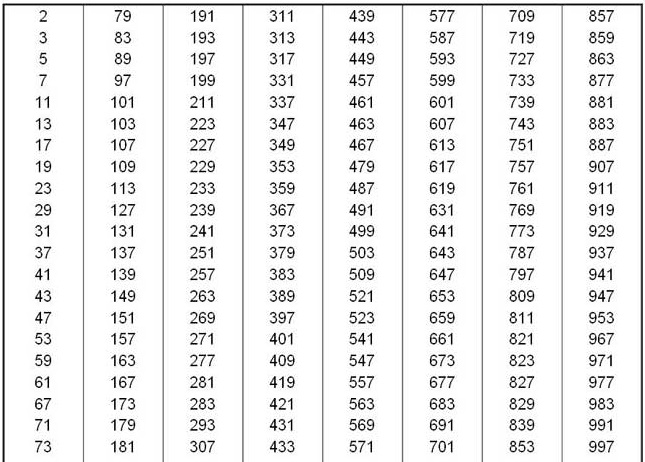
3. Bảng số nguyên tố (nhỏ hơn 1000)
Trả lời câu hỏi bài 14 trang 46 SGK toán lớp 6
Trong các số 7, 8, 9, số nào là số nguyên tố, số nào là hợp số ? Vì sao ?
Giải:
– Số 7 là số nguyên tố vì 7 là số tự nhiên lớn hơn 1 và có hai ước là 1 và chính nó.
– Số 8 là hợp số vì 8 là số tự nhiên lớn hơn 1 và có nhiều hơn hai ước đó là 1; 2; 4; 8.
– Số 9 là hợp số vì 9 là số tự nhiên lớn hơn 1 và có nhiều hai ước là 1; 3; 9.
Giải bài tập bài 14 trang 46 Toán 6 Tập 1
Bài 115 trang 47 SGK Toán 6 Tập 1
Các số sau là số nguyên tố hay hợp tố ?
312; 213; 435; 417; 3311; 67.
Giải:
Muốn biết một số có phải số nguyên tố hay không ta phải xem nó có bao nhiêu ước. Vậy nếu ta biết một số có nhiều hơn 2 ước là 1 và chính nó thì số đó chắn chắn là hợp số mà không cần phải tìm hết các ước của nó.
Ta có 3 + 1 + 2 = 6 chia hết cho 3 nên 312 ⋮3; nghĩa là 312 có ước là 3, khác 1 và 312. Vậy 312 là một hợp số.
Tương tự 213 cũng là một hợp số.
435 là một hợp số vì 435⋮5.
Vì 3311 = 11.301 nên 3311 có ước là 11 và 301. Vậy 3311 cũng là một hợp số.
67 là một số nguyên tố vì nó chỉ có hai ước là 1 và 67.
Bài 116 trang 47 SGK Toán 6 Tập 1
Gọi P là tập hợp các số nguyên tố. Điền kí hiệu ∈, ∉ hoặc ⊂ vào ô vuông cho đúng:
83 P , 91 P, 15 N , P N.
Giải:
83 ∈ P, 91 ∉ P, 15 ∈ N, P ⊂ N.
Bài 117 trang 47 SGK Toán 6 Tập 1
Dùng bảng số nguyên tố ở cuối sách, tìm các số nguyên tố trong các số sau:
117; 131; 313; 469; 647.
Giải:
131, 313, 647.
Bài 118 trang 47 SGK Toán 6 Tập 1
Tổng (hiệu) sau là số nguyên tố hay hợp tố ?
a) 3.4.5 + 6.7; b) 7.9.11.13 – 2.3.4 .7;
c) 3.5.7 + 11.13.17; d) 16354 + 67541.
Giải:
a) Ta có 3.4.5 và 6.7 đều chia hết cho 6 nên 3.4.5 + 6.7 chia hết cho 6 vậy là 3.4.5 + 6.7 một hợp số vì có nhiều hơn 2 ước.
b) Tương tự ta có 7.9.11.13 – 2.3.4.7 chia hết cho 7 nên 7.9.11.13 – 2.3.4.7 là một hợp số.
c) Ta có 3.5.7 + 11.13.17 là một số chẵn nên chia hết cho 2.
Vậy 3.5.7 + 11.13.17 là một hợp số.
d) Ta có 16354 + 67541 là tổng có số tận cùng bởi chữ số 5 nên chia hết cho 5.
Vậy 16354 + 67541 là một hợp số.
Bài 119 trang 47 SGK Toán 6 Tập 1
Thay chữ số vào dấu * để được hợp số: \[ \overline {1*}\]; \[ \overline {3*}\]
Giải:
Ta có 02 cách để giải bài này:
Cách 1: Xét xem mỗi số từ 10 đến 19 và từ 30 đến 39 xem số nào có ước khác 1 và chính nó.
Cách 2: Dùng bảng số nguyên tố ở cuối sách giáo khoa đề loại bỏ các số nguyên tố trong khoảng từ 10 đến 19 và từ 30 đến 39.
Đương nhiên là đối với cách 2 ta sẽ dễ dàng hơn. Tra bảng các số nguyên tố ta có 11, 13, 17, 19, 31, 37 là các số nguyên tố. Vậy:
– Các hợp số có dạng \[ \overline {1*}\] là 12 ; 14 ; 15 ; 16 ; 18.
– Các hợp số có dạng \[ \overline {3*}\] là: 30; 32; 33 ; 34 ; 35 ; 36 ; 38 ; 39.
Bài viết liên quan