Ghi số tự nhiên là nội dung bài 3 SGK lớp 6 trang 8, 9, 10, 11. Bạn cần phải nắm lý thuyết về số và chữ số, hệ thập phân là gì, cách ghi số la mã và cách ghi số trong hệ nhị phân. Đây là bài học rất quan trọng trong môn toán số học. Do đó, các bạn phải hiểu rõ và giải được những bài toán liên quan.
Tóm tắt nội dung
Lý thuyết bài 3. Ghi số tự nhiên
1. Số và chữ số
Một số tự nhiên có thể có một, hai, ba,…chữ số. Bởi vì không có số tự nhiên lớn nhất nên chữ số của số tự nhiên cũng là vô hạn.
Ví dụ:
9 là một số có một chữ số.
39 là một số có hai chữ số.
952 là một số có ba chữ số.
5279 là một số có bốn chữ số.
Chú ý:
– Chữ số đầu tiên của một số tự nhiên luôn khác không. Ví dụ: số 0123 không phải là một số có bốn chữ số mà thực chất chỉ là số 123, là một số có ba chữ số.
– Khi viết một số tự nhiên có bốn chữ số trở lên, người ta thường viết tách riêng ra thành từng nhóm có 3 chữ số kể từ phải sang trái cho dễ đọc.
Chẳng hạn như: Số 38526879 sẽ tách ra là 38 526 879 để dễ phân biệt hàng nghìn cho dễ đọc.
2. Hệ thập phân
Trong hệ thập phân, để ghi số tự nhiên người ta dùng mười chữ số là: 0; 1; 2; 3; 4; 5; 6; 7; 8; 9.
Cứ mười đơn vị của một hàng thì làm thành một đơn vị của hàng liền trước đó.
Kí hiệu: \[ \overline {ab}\] chỉ số tự nhiên có hai chữ số, chữ số hàng chục là a, chữ số hàng đơn vị là b. Như vậy \[ \overline {ab}\] = a.10 + b
\[ \overline {abc}\] là số tự nhiên có ba chữ số, chữ số hàng trăm là a, chữ số hàng chục là b, chữ số hàng đơn vị là c. Như vậy \[ \overline {abc}\] = a.100 + b.10 + c
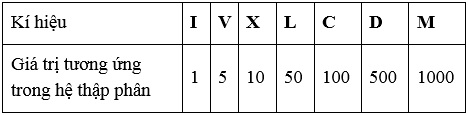
3. Cách ghi số La Mã
* Số La Mã gồm có 7 chữ số:
Ví dụ: Số XIV tương ứng là số 14.
Số XXVI tương ứng là số 26.
* Quy tắc là:
– Mỗi chữ số La Mã không viết liền nhau quá ba lần.
– Chữ số có giá trị nhỏ đứng trước chữ số có giá trị lớn làm giảm giá trị của chữ số có giá trị lớn. Ví dụ: Số La Mã IV; IX; XL; XC; XD có giá trị trong hệ thập phân tương ứng là 4; 9; 40; 90; 400; 900.
4. Cách ghi số trong hệ nhị phân
Để ghi số trong hệ nhị phân ta chỉ dùng 2 chữ số là: 0 và 1.
Ví dụ:
– Trong hệ nhị phân: 1101 = 1. 23 + 1.22+ 0. 21 + 1. 20 = 13 trong hệ thập phân.
– Số 8 trong hệ thập phân sẽ là 8 = 1. 23 + 0. 22 + 0. 21 + 0. 20 = 1000 trong hệ nhị phân.
Trả lời câu hỏi bài 3 trang 9, SGK Toán 6 Tập 1
Hãy viết:
– Số tự nhiên lớn nhất có ba chữ số
– Số tự nhiên lớn nhất có ba chữ số khác nhau.
Giải:
– Số tự nhiên lớn nhất có ba chữ số là số 999.
– Số tự nhiên lớn nhất có ba chữ số khác nhau là số 987.
Giải bài tập 11,12,13,14,15 trang 10, SGK Toán 6 Tập 1
Bài 11 trang 10, SGK Toán 6 Tập 1
a) Viết số tự nhiên có số chục là 135, chữ số hàng đơn vị là 7
b) Điền vào bảng:
Giải:
a) Số tự nhiên có số chục là 135, chữ số hàng đơn vị là 7: là số 1357. Ta có thể tính như sau: 135.10 + 7 = 1357
b)

Bài 12 trang 10, SGK Toán 6 Tập 1
Viết tập hợp các chữ số của số 2000.
Giải: Số 2000 có bốn chữ số là chữ số 2 và ba chữ số 0.
Tuy nhiên khi viết một tập hợp thì mỗi phần tử chỉ được liệt kê một lần nên tập hợp các chữ số của số 2000 sẽ là {0; 2}.
Bài 13 trang 10, SGK Toán 6 Tập 1
a) Viết số tự nhiên nhỏ nhất có bốn chữ số.
b) Viết số tự nhiên nhỏ nhất có bốn chữsố khác nhau.
Giải:
a) Số nhỏ nhất có bốn chữ số là 1000.
Lý giải: Một số có bốn chữ số là số nhỏ nhất thì chữ số đầu tiên của nó phải là số nhỏ nhất khác 0 (tức số 1), các chữ số còn lại là số nhỏ nhất (tức số 0). Vì thế số có bốn chữ số nhỏ nhất là 1000.
b) Số nhỏ nhất có bốn chữ số khác nhau là 1023.
Lý giải: Một số có bốn chữ số khác nhau là số nhỏ nhất thì chữ số đầu tiên của nó phải là số nhỏ nhất khác 0 (tức số 1); chữ số kế tiếp phải là số nhỏ nhất khác 1 (tức số 0); chữ số kế tiếp phải là số nhỏ nhất khác 0 và 1 (tức số 2); và chữ số hàng đơn vị phải là 3.
Vậy số tự nhiên nhỏ nhất có bốn chữ ố khác nhau là 1023.
Bài 14 trang 10, SGK Toán 6 Tập 1
Dùng ba chữ số 0, 1, 2, hãy viết tất cả các số tự nhiên có ba chữ số mà các chữ số khác nhau.
Các số tự nhiên có ba chữ số 0,1,2 mà các chữ số khác nhau đó là: 102; 120; 201; 210
Lý giải: Vì số có ba chữ số nên chữ số hàng trăm phải khác 0. Do đó chữ số hàng trăm chỉ có thể là 1 hoặc 2. Vậy ta viết tất cả các số có chữ số hàng trăm là 1 và các chữ số còn lại là 0 và 2; sau đó ta tiếp tục viết tất cả các số có chữ số hàng trăm là 2 và các chữ số còn lại là 0 và 1.
Đáp số: 102; 120; 201; 210.
Bài 15 trang 10, SGK Toán 6 Tập 1
a) Đọc các số La Mã sau: XIV; XXVI.
b) Viết các số sau bằng số La Mã: 17; 25
c) Cho chín que diêm được sắp xếp như trên hình 8. Hãy chuyển chỗ một que diêm để được kết quả đúng.

Giải:
a) XIV = 10 + 4 = 14;
XXVI = 10 + 10 + 5 + 1 = 26.
b) 17 = 10 + 5 + 1 + 1 = XVII;
25 = 10 + 10 + 5 = XXV.
c) Trong hình vẽ ta có phép tính 6 = 5 – 1. Là một hép tính sai.
Ta có một số cách di chuyển que diêm để được phép tính đúng như sau:
Cách 1: Di chuyển vị trí que diêm thứ 3 (tính từ trái qua) ta được phép tính 4 = 5 – 1.
Cách 2: Di chuyền vị trí que diêm thứ 3 (tính từ trái qua) ta được: 5 = 6 – 1.

Cách 3: Di chuyển vị trí que diêm thứ 3 (tính từ trái qua) ta được: 5 ≠ 5 – 1.
Cách 4: Di chuyển vị trí que diêm ở dấu bằng ta được: 6 – 5 = 1.
Bài viết liên quan